Difference between revisions of "- Spin-Lattice Relaxation Time"
(→Spin-Lattice Relaxation Time) |
(→Spin-Lattice Relaxation Time) |
||
| Line 38: | Line 38: | ||
<math>\frac{dn}{dt}=2N_{_-}W_{_-}-2N_{_+}W_{_+}</math> . Using the previously found expressions for <math>W_{_+} \text{and } W_{_-}</math> this becomes | <math>\frac{dn}{dt}=2N_{_-}W_{_-}-2N_{_+}W_{_+}</math> . Using the previously found expressions for <math>W_{_+} \text{and } W_{_-}</math> this becomes | ||
| − | <math>\frac{dn}{dt}=2W(n_0-n)</math>, where <math>n_0=\frac{N\mu H_{_0}}{kT}</math> is the value of <math>n</math> when the spin system is in thermal equilibrium with the lattice. | + | <math>\frac{dn}{dt}=2W(n_0-n)</math>, where <math>n_0=\frac{N\mu H_{_0}}{kT}</math> is the value of <math>n</math> when the spin system is in thermal equilibrium with the lattice. This implies that <math>T</math>, the lattice temperature, is associated with the excess population <math>n_{_0}</math> at thermal equilibrium. |
The equation for <math>\frac{dn}{dt}</math> can be directly integrated to give | The equation for <math>\frac{dn}{dt}</math> can be directly integrated to give | ||
Latest revision as of 11:54, 15 February 2019
Spin-Lattice Relaxation Time
Definition: (Lattice) The material in which the nuclear magnets are embedded is generally referred to as the lattice, whether it be solid, liquid or gas.
Let us now consider an assembly of identical spin-1/2 nuclei in the presence of a steady magnetic field . Assume that there is only weak coupling between the nuclear spins. This assumption allows us to consider that the spin energy levels of the assembly are the same as that for a single spin. Although we assume weak coupling between the spins the coupling must not be zero. That is, the weak coupling between the spins must at least be sufficient enough to bring about thermal equilibrium between the spins. Furthermore, suppose that the interaction between the nuclear spins and the lattice is even smaller than the interaction between spins. This means that, apart from the feeble paramagnetism produced by the nuclei, the material concerned must be diamagnetic (water is diamagnetic).
Each nucleus has two possible energy levels separated by a gap of . Suppose we apply radiation of the resonant frequency polarized in a direction perpendicular to , transitions between energy levels then take place. From the theory of the Einstein coefficients the probability of an upwards transition (by absorption) equals the probability of a downward transition (by stimulated emission). In comparison, the probability of a downward transition (by spontaneous emission) is found to be negligible (Purcell 1946).
If the numbers of nuclei in each energy level were equal, the average rate of transitions up and down would be equal and no net effect would be observed on the system. However, since the nuclear spins are in equilibrium at temperature the population of the lower level exceeds that of the upper level by the Boltzmann Factor , where is Boltzmann's constant.
At room temperature, for protons in a field of 5000 Gauss, this factor has the value of . Because of this typically small, but finite, excess population in the lower energy state, there is a net absorption of energy from the transverse RF field. The absorption of energy corresponds to the transfer of some of the excess population in the lower level to the upper level. Assuming no lattice-spin interaction, the fractional excess of the lower level population steadily dwindles. This implies that the spin system's temperature is steadily rising due to a process of RF heating. The temperature of the lattice, however, is not affected since we assumed negligible lattice-spin interaction. In this case we can speak separately of 'spin temperature'and 'lattice temperature'.
In a real physical system, the nuclear spins are never entirely bereft of interaction with the lattice (although the interaction is very often quite small). Such interaction as there is tends to bring both spin and lattice into thermal equilibrium at the same temperature. In practice, this temperature is quite close to the lattice temperature (the heat capacity of the lattice is much greater than the heat capacity of the spins - except at very low temperatures).
So, while the RF radiation is reducing the excess population of the lower level, the interactions with the lattice are tending to restore the lower-level excess population to its original value.
Now suppose that the spin temperature is initially equal to that of the lattice, and we suddenly raise it to a value greater than the lattice temperature by application of the transverse RF field. If this field is suddenly removed, we may now ask how rapidly will the spin temperature return to that of the lattice?
In order that the spin system may cool down to the temperature of the lattice there must be a net downward transfer of nuclei to the lower energy level. Since the population of the upper level does not exceed that of the lower level, this can only be possible if the probability of a downward transition exceeds that of an upward transition. Remember that here we're talking about transitions between energy levels in the absence of an applied transverse field (so Einstein coefficient arguments don't apply).
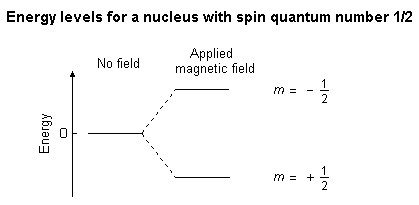
Recall the energy levels for a spin-1/2 particle in a magnetic field (shown below).
Suppose that the number density of nuclei in the upper/lower energy state is . Let be the probability of a downward/upward transition. If the whole spin-lattice system is in thermal equilibrium at temperature , then .
In equilibrium are related by the Boltzmann factor so that . If we let , where is the average transition rate of the upper and lower transitions. Then .
So, . Similarly, .
And we have that the two transitions rates out of the two levels are not the same, with the transition rate out of the upper level greater than that for the lower level .
This makes sense physically because a lattice center can give up a quantum of energy only if it's in an excited state while a lattice center can accept a quantum of energy in any state (Bloembergen).
If we now consider the spin system at a temperature different from the lattice temperature and , the excess number of nuclei in the lower state, we see that changes by 2 with each transition so that
. Using the previously found expressions for this becomes
, where is the value of when the spin system is in thermal equilibrium with the lattice. This implies that , the lattice temperature, is associated with the excess population at thermal equilibrium.
The equation for can be directly integrated to give
, where is the initial value of (the excess number of nuclei in the lower state).
This shows that equilibrium is approached exponentially with a characteristic time of
.
The approach of the spin and lattice systems to equilibrium can be termed a thermal relaxation process, and for this reason, is called the spin-lattice relaxation time or the thermal relaxation time. Bloch (1946) has given the alternative name of longitudinal relaxation time.
The detailed nature of the spin-lattice interaction and the theoretical evaluation of is discussed further in Andrew's book Nuclear Magnetic Resonance. However, it is usually the case that the values of encountered experimentally range from to seconds. Itis usually longer for solids than for liquids and gases.
The presence of paramagnetic ions (e.g., KMnO4) in a liquid promotes the relaxation process and can reduce .