Difference between revisions of "Interferometers"
| Line 22: | Line 22: | ||
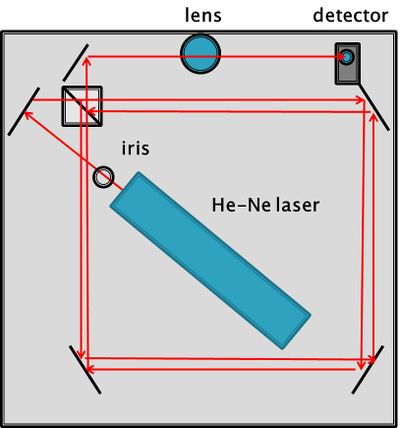
The Setup of the Sagnac interferometer is shown in figure 5. | The Setup of the Sagnac interferometer is shown in figure 5. | ||
| − | [[File:giraffe.jpg|400px|right|thumb|Figure 2: Setup of the | + | [[File:giraffe.jpg|400px|right|thumb|Figure 2: Setup of the Sagnac Interferometer. The extra mirror behind the beam splitter added to fit detector and lens on rotating platform]] |
To rotate the interferometer, it was placed on a rotating stool. The power source and digital oscilloscope were place on another platform above the interferometer (Figure 6). | To rotate the interferometer, it was placed on a rotating stool. The power source and digital oscilloscope were place on another platform above the interferometer (Figure 6). | ||
The Sagnac interferometer was intended to verify the wavelength of the He-Ne laser. This would be accomplished with the relations z=(4*omega*A)/(lambda*c) and P(t)=(Pin/2)(1+cos(z(t)). Here z is the phase-change, omega is the angular velocity of the rotating platform, A is the area enclosed by the interferometer arms, and P(t) is the photocurrent. | The Sagnac interferometer was intended to verify the wavelength of the He-Ne laser. This would be accomplished with the relations z=(4*omega*A)/(lambda*c) and P(t)=(Pin/2)(1+cos(z(t)). Here z is the phase-change, omega is the angular velocity of the rotating platform, A is the area enclosed by the interferometer arms, and P(t) is the photocurrent. | ||
Revision as of 15:21, 21 March 2014
The goal of the spectroscopy project was to create a michelson, mach-zehnder and sagnac Interferometer. Each setup utilized a 632.8nm Helium-Neon laser.
In order to reduce fringe-drift, the michelson interferometer employed both an optical iris and an optical isolator. The setup of the michelson interferometer is shown in Figure 1.
The Michelson interferometer was used to measure both the "voltage-to-expansion" ratio of a PZT and the coherence length of the He-Ne laser.
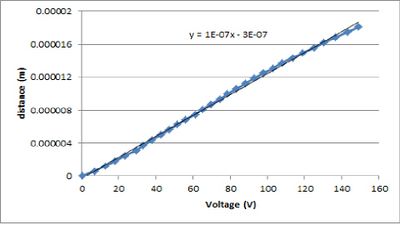
To measure the "voltage-to-expansion" ratio, the PZT was wedged in the track of he adjustable mirror. By increasing the voltage across the PZT and simultaneously counting the number of fringes that passed an arbitrary point on the projection screen, it was possible to measure the expansion distance of the PZT using the relation d=m*lambda/2. Multiple measurements were recorded and plotted in Figure 2.
The slope of the graph indicates the PZT expands at a rate 100nm/Volt.
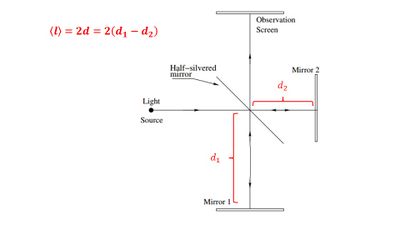
To measure the coherence length of the He-Ne laser, mirror 1 was gradually moved backwards until the interference pattern was no longer visible. The coherence length <l>, is given by the relation <l>=2*d, where d is the difference in length between the arms of the interferometer (Figure 3). The coherence length was determined to be 78cm.
The mach-zehnder interferometer setup is shown in Figure 4.
As with the Michelson interferometer, an optial iris was employed to minimize outside noise. However, the optical isolator proved unnecessary with the Mach-Zehnder interferometer as no fringe drift was observed.
The Setup of the Sagnac interferometer is shown in figure 5.
To rotate the interferometer, it was placed on a rotating stool. The power source and digital oscilloscope were place on another platform above the interferometer (Figure 6).
The Sagnac interferometer was intended to verify the wavelength of the He-Ne laser. This would be accomplished with the relations z=(4*omega*A)/(lambda*c) and P(t)=(Pin/2)(1+cos(z(t)). Here z is the phase-change, omega is the angular velocity of the rotating platform, A is the area enclosed by the interferometer arms, and P(t) is the photocurrent.