Difference between revisions of "Pound Drever Hall Lock-In"
(added PDH diagram pic) |
(edited minor error in content) |
||
| Line 7: | Line 7: | ||
=== Theory === | === Theory === | ||
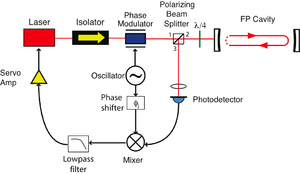
[[File:PDHBasicLayout.png|thumbnail|Basic PDH Setup]] | [[File:PDHBasicLayout.png|thumbnail|Basic PDH Setup]] | ||
| − | The main concept behind the PHD lock-in method is the use of a Cavity to sense the laser frequency and then adjust the laser based on the laser-cavity frequency difference. The basic way of using a Cavity to measure a lasers frequency is by measuring the transmission or reflection of the cavity at different cavity lengths. Since, the objective is to set the laser to a stabilize a laser around a single frequency, the cavity length will not change. The frequency measurement should also be from the reflected beam of the cavity, so transmitted beam may used. If the cavity resonance is near the laser wavelength, then the reflectance can be approximated by a quadratic function. Though, you can't lock a laser to just the reflected beam because if the laser is slightly off resonance with the cavity there is no way to tell if the laser frequency is higher or lower than the cavity, you can only tell that the laser is off resonance. To fix this note that the derivative of a quadratic function is linear and therefore would fix the frequency ambiguity of the quadratic function. Now, in order to sense the derivative of the reflected beam, with respect to frequency, the laser needs to have is frequency varied. The reason for varying the laser frequency, is to allow for a discrete approximation of a derivative. This means that the reflected beam will have three frequencies, each with there own intensities, based on the reflectance at the respective frequencies. Therefore, when the reflected beam hits the detector, the detector will detect a beat frequency. This beat frequency will create | + | The main concept behind the PHD lock-in method is the use of a Cavity to sense the laser frequency and then adjust the laser based on the laser-cavity frequency difference. The basic way of using a Cavity to measure a lasers frequency is by measuring the transmission or reflection of the cavity at different cavity lengths. Since, the objective is to set the laser to a stabilize a laser around a single frequency, the cavity length will not change. The frequency measurement should also be from the reflected beam of the cavity, so transmitted beam may used. If the cavity resonance is near the laser wavelength, then the reflectance can be approximated by a quadratic function. Though, you can't lock a laser to just the reflected beam because if the laser is slightly off resonance with the cavity there is no way to tell if the laser frequency is higher or lower than the cavity, you can only tell that the laser is off resonance. To fix this note that the derivative of a quadratic function is linear and therefore would fix the frequency ambiguity of the quadratic function. Now, in order to sense the derivative of the reflected beam, with respect to frequency, the laser needs to have is frequency varied. The reason for varying the laser frequency, is to allow for a discrete approximation of a derivative. This means that the reflected beam will have three frequencies, each with there own intensities, based on the reflectance at the respective frequencies. Therefore, when the reflected beam hits the detector, the detector will detect a beat frequency. This beat frequency will create AC signals based on the frequency interaction. In order to know what side of the cavity resonance the laser is on, an analysis of the cavities effect of the lasers side bands is needed. The detector will output quite a few frequencies, but the ones of interest are oscillating at frequency that the laser is being driven at, i.e. the side band beat frequency. to turn these AC signals into a DC signal the use of a mixer is needed, this is to turn the desired ac frequency into (ac)^2. This trick allows the use of the Trig Identity Cos(wt)^2 = 1 + Cos(2wt) to be used, meaning that with the addition of a low pass filter, a DC based of the magnitude of the the sideband that gets reflected the most is obtained. |
=== Our Setup === | === Our Setup === | ||
Revision as of 12:49, 12 March 2014
Contents
Pound Drever Hall Lock-In Project
Overview
The Pound Drever Hall, or PDH, Lock-In Project is desinged to prepare students for working with tunable lasers, high frequency electronics, and optical Cavities. The objective of this project, as the name entails, is to uses the PHD technique to lock a tunable laser to a cavity. Both the laser and the cavity will be constructed by the students using suplied parts, allowing the students to learn the theory behind tunable lasers and the logistics of constucting an optical cavity.
Theory
The main concept behind the PHD lock-in method is the use of a Cavity to sense the laser frequency and then adjust the laser based on the laser-cavity frequency difference. The basic way of using a Cavity to measure a lasers frequency is by measuring the transmission or reflection of the cavity at different cavity lengths. Since, the objective is to set the laser to a stabilize a laser around a single frequency, the cavity length will not change. The frequency measurement should also be from the reflected beam of the cavity, so transmitted beam may used. If the cavity resonance is near the laser wavelength, then the reflectance can be approximated by a quadratic function. Though, you can't lock a laser to just the reflected beam because if the laser is slightly off resonance with the cavity there is no way to tell if the laser frequency is higher or lower than the cavity, you can only tell that the laser is off resonance. To fix this note that the derivative of a quadratic function is linear and therefore would fix the frequency ambiguity of the quadratic function. Now, in order to sense the derivative of the reflected beam, with respect to frequency, the laser needs to have is frequency varied. The reason for varying the laser frequency, is to allow for a discrete approximation of a derivative. This means that the reflected beam will have three frequencies, each with there own intensities, based on the reflectance at the respective frequencies. Therefore, when the reflected beam hits the detector, the detector will detect a beat frequency. This beat frequency will create AC signals based on the frequency interaction. In order to know what side of the cavity resonance the laser is on, an analysis of the cavities effect of the lasers side bands is needed. The detector will output quite a few frequencies, but the ones of interest are oscillating at frequency that the laser is being driven at, i.e. the side band beat frequency. to turn these AC signals into a DC signal the use of a mixer is needed, this is to turn the desired ac frequency into (ac)^2. This trick allows the use of the Trig Identity Cos(wt)^2 = 1 + Cos(2wt) to be used, meaning that with the addition of a low pass filter, a DC based of the magnitude of the the sideband that gets reflected the most is obtained.