Difference between revisions of "- The Resonance Condition"
| (5 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Consider an isolated nucleus in a steady magnetic field <math>H_{_0}</math>. The magnetic field breaks the symmetry of free space and defines a particular spatial direction. Suppose that the nucleus possesses an intrinsic "spin" with spin number <math>I>0</math> so that it has an intrinsic magnetic moment (moving/spinning electric charge creates a magnetic field). How does this intrinsic "spin" relate to angular momentum? It is necessary to find this relation explicitly. | Consider an isolated nucleus in a steady magnetic field <math>H_{_0}</math>. The magnetic field breaks the symmetry of free space and defines a particular spatial direction. Suppose that the nucleus possesses an intrinsic "spin" with spin number <math>I>0</math> so that it has an intrinsic magnetic moment (moving/spinning electric charge creates a magnetic field). How does this intrinsic "spin" relate to angular momentum? It is necessary to find this relation explicitly. | ||
| + | |||
| + | Definitions: The steady, strong magnetic field <math>H_{_0} </math> will be referred to as the ''longitudinal field''. The oscillating magnetic field applied perpendicular to <math>H_{_0}</math> will be called the ''transverse magnetic field''. | ||
We know from quantum mechanics that (on small enough scales) energy appears in discrete bits ( <math>\hbar</math> shows its face ). It is then reasonable to suppose that "spin" energies are also discrete (or quantized). Physical experiments bear out this supposition. | We know from quantum mechanics that (on small enough scales) energy appears in discrete bits ( <math>\hbar</math> shows its face ). It is then reasonable to suppose that "spin" energies are also discrete (or quantized). Physical experiments bear out this supposition. | ||
| Line 16: | Line 18: | ||
Correspondingly, the nuclear magnetic moment also has <math>(2I+1)</math> components in proportion. This is a consequence of "space quantization" demonstrated so famously by Stern and Gerlach in 1922. | Correspondingly, the nuclear magnetic moment also has <math>(2I+1)</math> components in proportion. This is a consequence of "space quantization" demonstrated so famously by Stern and Gerlach in 1922. | ||
| − | We can define <math>\mu</math> as the maximum measurable (observable) component of the magnetic moment. Even though the length of the magnetic moment vector is <math>[(I+1)/I]^{1/2}\mu </math>, the quantity of physical interest is <math>\mu</math> and for this reason workers in the field usually refer to <math>\mu</math> as ''the magnetic moment''. As mentioned above, the energy levels of the nuclear magnet in the | + | We can define <math>\mu</math> as the maximum measurable (observable) component of the magnetic moment. Even though the length of the magnetic moment vector is <math>[(I+1)/I]^{1/2}\mu </math>, the quantity of physical interest is <math>\mu</math> and for this reason workers in the field usually refer to <math>\mu</math> as ''the magnetic moment''. As mentioned above, the energy levels of the nuclear magnet in the field <math>H_{_0}</math> are given by the <math>(2I+1)</math> values of <math>\tfrac{-m\mu H_{_0}}{I}</math>. In the general case, this results in a set of equally-spaced levels with separation <math>\tfrac{\mu H_{_0}}{I}</math> between adjacent levels. |
---- | ---- | ||
| − | This separation is often written as <math>g \mu_{_0} H_{_0}</math>, where <math>g=\ | + | This separation is often written as <math>g \mu_{_0} H_{_0}</math>, where <math>g=\tfrac{\mu}{\mu_{_0}I}</math> is called the ''splitting factor'' or the ''g-factor''. The selection rules (derived from energy and momentum conservation arguments), state that <math>m</math> can change by <math>\pm 1</math>. Transitions that involve a change of <math>m</math> by <math>\pm 1</math> require (or produce) circularly polarized light (for momentum conservation). |
'''A quantum of energy <math>\lambda</math> can therefore excite transitions between levels if it has the same energy as the level spacing and is circularly polarized. That is, if <math>h\nu_{_0}=g\mu_{_0}H_{_0}</math>, where <math>\nu_{_0}</math> is the frequency of the electromagnetic radiation supplying the quanta of energy and its magnetic field is circularly polarized in the plane perpendicular to the steady magnetic field .''' | '''A quantum of energy <math>\lambda</math> can therefore excite transitions between levels if it has the same energy as the level spacing and is circularly polarized. That is, if <math>h\nu_{_0}=g\mu_{_0}H_{_0}</math>, where <math>\nu_{_0}</math> is the frequency of the electromagnetic radiation supplying the quanta of energy and its magnetic field is circularly polarized in the plane perpendicular to the steady magnetic field .''' | ||
| Line 25: | Line 27: | ||
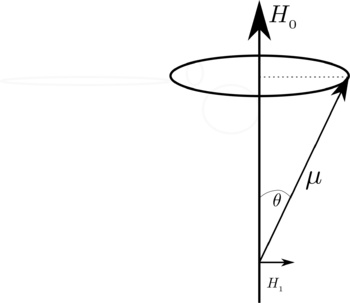
For a proton the value of <math>g</math> is ~ 5.58. Therefore, in a field of 5000 Gauss, the resonance frequency is ~ 21.3MHz. This satisfies energy conservation requirements. To understand the polarization requirements consider the figure below. | For a proton the value of <math>g</math> is ~ 5.58. Therefore, in a field of 5000 Gauss, the resonance frequency is ~ 21.3MHz. This satisfies energy conservation requirements. To understand the polarization requirements consider the figure below. | ||
| − | [[File:Circ.png| | + | [[File:Circ.png| 350px]] |
Consider a magnetic dipole <math>\mu</math> placed in a magnetic field <math>H_{_0}</math> as shown above. The dipole precesses about the direction of <math>H_{_0}</math>. The rate of precession is given by the well-known Larmor frequency <math>\omega_{_0}=\gamma H_{_0}</math>. Now suppose that an additional small magnetic field <math>H_{_1}</math> is applied at right angles to <math>H_{_0}</math> This "transverse" field will tend to cause <math>\mu</math> to increase its angle <math>\theta</math> (increasing the dipole's energy). If the small field <math>H_{_1}</math> is made to rotate around the axis defined by <math>H_{_0}</math> at the same frequency as that at which the dipole <math>\mu</math> precesses (the Larmor frequency) then the field <math>H_{_1}</math> will cause the angle <math>\theta</math> to steadily increase (adding energy to the nucleon). | Consider a magnetic dipole <math>\mu</math> placed in a magnetic field <math>H_{_0}</math> as shown above. The dipole precesses about the direction of <math>H_{_0}</math>. The rate of precession is given by the well-known Larmor frequency <math>\omega_{_0}=\gamma H_{_0}</math>. Now suppose that an additional small magnetic field <math>H_{_1}</math> is applied at right angles to <math>H_{_0}</math> This "transverse" field will tend to cause <math>\mu</math> to increase its angle <math>\theta</math> (increasing the dipole's energy). If the small field <math>H_{_1}</math> is made to rotate around the axis defined by <math>H_{_0}</math> at the same frequency as that at which the dipole <math>\mu</math> precesses (the Larmor frequency) then the field <math>H_{_1}</math> will cause the angle <math>\theta</math> to steadily increase (adding energy to the nucleon). | ||
| − | A resonance therefore occurs when the angular frequency of the transverse field is equal to the dipole's Larmor precession frequency. This | + | A resonance therefore occurs when the angular frequency of the transverse field is equal to the dipole's Larmor precession frequency. Although a rotating transverse magnetic field is quite practicable, |
| + | it is usually much simpler to provide a linearly oscillating field. That is because a linearly oscillating field may be regarded as the superposition of two rotating fields. Resonance occurs when one of these two rotating fields has the correct rotation direction (with respect to the precessing dipole). It is generally not possible to tell which rotating field component (CW or CCW) is utilized. This information is only required when it is desired to find the sign of <math>\mu</math>, which determines the direction of Larmor precession. | ||
Latest revision as of 18:30, 13 February 2019
The Resonance Condition
Consider an isolated nucleus in a steady magnetic field . The magnetic field breaks the symmetry of free space and defines a particular spatial direction. Suppose that the nucleus possesses an intrinsic "spin" with spin number so that it has an intrinsic magnetic moment (moving/spinning electric charge creates a magnetic field). How does this intrinsic "spin" relate to angular momentum? It is necessary to find this relation explicitly.
Definitions: The steady, strong magnetic field will be referred to as the longitudinal field. The oscillating magnetic field applied perpendicular to will be called the transverse magnetic field.
We know from quantum mechanics that (on small enough scales) energy appears in discrete bits ( shows its face ). It is then reasonable to suppose that "spin" energies are also discrete (or quantized). Physical experiments bear out this supposition.
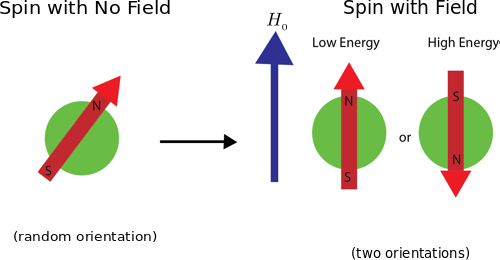
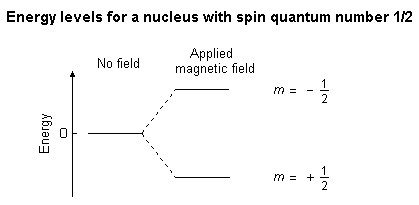
The nucleus will have different energy states depending on the magnitude and direction of the nucleon's magnetic moment. See the figure below for the allowed spin states of a spin-1/2 particle.
The energy of a magnetic moment in a magnetic field is . If the energy in the system is low enough, most, if not all, of the spins will be parallel to the field (lowest energy state). However, if there is enough energy around then some nucleons will absorb a bit of energy and will become aligned anti-parallel to the magnetic field.
A careful study of quantum mechanics reveals that the length of the nuclear angular momentum vector is but that the only measurable components of this vector are given by , where , the magnetic quantum number, may take any of the values in the series .
![{\displaystyle [I(I+1)]^{1/2}\hbar }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ab134e30271f2490d101ce9e10aef3314b00c32)
Correspondingly, the nuclear magnetic moment also has components in proportion. This is a consequence of "space quantization" demonstrated so famously by Stern and Gerlach in 1922.
We can define as the maximum measurable (observable) component of the magnetic moment. Even though the length of the magnetic moment vector is , the quantity of physical interest is and for this reason workers in the field usually refer to as the magnetic moment. As mentioned above, the energy levels of the nuclear magnet in the field are given by the values of . In the general case, this results in a set of equally-spaced levels with separation between adjacent levels.
![{\displaystyle [(I+1)/I]^{1/2}\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f79a86c4c790dee4dd076f2fa6e4468e92cf88)
This separation is often written as , where is called the splitting factor or the g-factor. The selection rules (derived from energy and momentum conservation arguments), state that can change by . Transitions that involve a change of by require (or produce) circularly polarized light (for momentum conservation).
A quantum of energy can therefore excite transitions between levels if it has the same energy as the level spacing and is circularly polarized. That is, if , where is the frequency of the electromagnetic radiation supplying the quanta of energy and its magnetic field is circularly polarized in the plane perpendicular to the steady magnetic field .
For a proton the value of is ~ 5.58. Therefore, in a field of 5000 Gauss, the resonance frequency is ~ 21.3MHz. This satisfies energy conservation requirements. To understand the polarization requirements consider the figure below.
Consider a magnetic dipole placed in a magnetic field as shown above. The dipole precesses about the direction of . The rate of precession is given by the well-known Larmor frequency . Now suppose that an additional small magnetic field is applied at right angles to This "transverse" field will tend to cause to increase its angle (increasing the dipole's energy). If the small field is made to rotate around the axis defined by at the same frequency as that at which the dipole precesses (the Larmor frequency) then the field will cause the angle to steadily increase (adding energy to the nucleon).
A resonance therefore occurs when the angular frequency of the transverse field is equal to the dipole's Larmor precession frequency. Although a rotating transverse magnetic field is quite practicable, it is usually much simpler to provide a linearly oscillating field. That is because a linearly oscillating field may be regarded as the superposition of two rotating fields. Resonance occurs when one of these two rotating fields has the correct rotation direction (with respect to the precessing dipole). It is generally not possible to tell which rotating field component (CW or CCW) is utilized. This information is only required when it is desired to find the sign of , which determines the direction of Larmor precession.
