Difference between revisions of "Function Generators and Oscilloscopes"
(→Circuit Setup) |
m |
||
| (158 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | Function generators and oscilloscopes will be covered as a pair. Oscilloscopes measures voltages as a function of time and displays the data on a graph. Function generators create a changing voltage under some function of time (often it is a sine wave, although there are a number of other shapes we'll see below). Thus, these two are natural to pair together. | + | [[File:FunGenAndOScope.png|300px|thumb|right|Rigol Function Generator (top) and Oscilloscope (bottom)]] |
| + | |||
| + | Function generators and oscilloscopes will be covered as a pair. Oscilloscopes measures voltages as a function of time and displays the data on a graph. Function generators create a changing voltage under some function of time (often it is a sine wave, although there are a number of other shapes we'll see below). Thus, these two are natural to pair together. Note that sometimes oscilloscope is shortened to "oscope" or just "scope". | ||
| + | |||
| + | This module will also review some circuit elements (diode operation), fourier analysis of a signal and data fitting to a function. | ||
| − | + | Each section has a table describing the function generator output setup for that section. Controls marked with an asterisk will be changed during that section. | |
| − | [[ | + | |
| − | + | This module is part of the [[General Lab Equipment Obstacle Course]]. | |
| + | == Equipment == | ||
| + | [[File:Bnc-adapters.png|300px|thumb|right|BNC-to-Banana Adapters: Socket (left) and Plug (right)]] | ||
| + | For this topic, you'll need the following equipment: | ||
<ul> | <ul> | ||
<li> Rigol DG1022 Function Generator</li> | <li> Rigol DG1022 Function Generator</li> | ||
<li> Rigol DS1102E Digital Oscilloscope</li> | <li> Rigol DS1102E Digital Oscilloscope</li> | ||
<li> 1kohm resistor</li> | <li> 1kohm resistor</li> | ||
| − | <li> 1uF | + | <li> 1uF capactitor</li> |
| + | <li> 1N4148 Diode</li> | ||
<li> Protoboard</li> | <li> Protoboard</li> | ||
<li> A number of short wires </li> | <li> A number of short wires </li> | ||
| − | <li> | + | <li> A few BNC-to-banana socket adapters (left adapter shown to right)</li> |
| − | <li> BNC-to-banana | + | <li> BNC-to-banana plug adapter (right adapter shown to right)</li> |
<li> Three BNC cables</li> | <li> Three BNC cables</li> | ||
<li> Two full sets of alligator clip - banana plug cables (that is a total of four cables with alligator clips on one end and banana plugs on the other) | <li> Two full sets of alligator clip - banana plug cables (that is a total of four cables with alligator clips on one end and banana plugs on the other) | ||
</ul> | </ul> | ||
| − | |||
| − | |||
== Circuit Setup == | == Circuit Setup == | ||
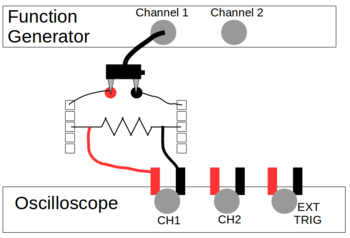
| − | [[File: | + | [[File:OscopeCir1.png|350px|right|thumbnail|<b>Circuit 1</b>: Simple Circuit for Function Generator/Oscilloscope]] |
We will need some circuit to read voltages from. Setup a circuit to run the output voltage of the function generator through your resistor and read the voltage dropped across the resistor with the oscilloscope. How to carefully set this up follows. | We will need some circuit to read voltages from. Setup a circuit to run the output voltage of the function generator through your resistor and read the voltage dropped across the resistor with the oscilloscope. How to carefully set this up follows. | ||
| Line 27: | Line 33: | ||
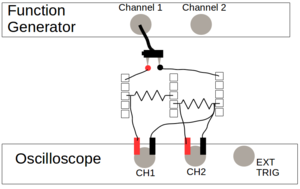
To bottom output of the function generator, plug in the BNC and attach the free end to the BNC-to-banana-plug adapter. The plastic cap on the banana-socket should unscrew slightly and reveal a hole underneath. For each socket, push the exposed end of a wire through the hole, then tighten down the cap to secure the wire to the socket. The wires should not go to the same row of holes in the protoboard. Connect the wire to a row on the protoboard, and plug the adapter into the sockets. The rows into which you plugged the wires should now be connected to the output of the function generator. Plug opposite ends of the resistor into the two rows of the protoboard that you have powered. Current that flows from the function generator should now travel through the resistor. | To bottom output of the function generator, plug in the BNC and attach the free end to the BNC-to-banana-plug adapter. The plastic cap on the banana-socket should unscrew slightly and reveal a hole underneath. For each socket, push the exposed end of a wire through the hole, then tighten down the cap to secure the wire to the socket. The wires should not go to the same row of holes in the protoboard. Connect the wire to a row on the protoboard, and plug the adapter into the sockets. The rows into which you plugged the wires should now be connected to the output of the function generator. Plug opposite ends of the resistor into the two rows of the protoboard that you have powered. Current that flows from the function generator should now travel through the resistor. | ||
| − | On each side of the resistor, attach an alligator clip. Attach a BNC-to-aligator-socket adapter to channel 1 of the oscilloscope. Plug the ends of the alligator clip into the banana-sockets. This should allow the oscilloscope to display, on channel 1, the voltage across the resistor, as shown | + | On each side of the resistor, attach an alligator clip. Attach a BNC-to-aligator-socket adapter to channel 1 of the oscilloscope. Plug the ends of the alligator clip into the banana-sockets. This should allow the oscilloscope to display, on channel 1, the voltage across the resistor, as shown to the right. |
| − | |||
| − | |||
== Oscilloscope Setup == | == Oscilloscope Setup == | ||
| Line 56: | Line 60: | ||
A yellow line of 0 volts is boring, so let's give the oscilloscope a signal to measure. | A yellow line of 0 volts is boring, so let's give the oscilloscope a signal to measure. | ||
| + | == Function Generator Setup == | ||
| − | = | + | {|class="wikitable floatright" |
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 20 Hz | ||
| + | | -- | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 0.5 V | ||
| + | | -- | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine | ||
| + | | OFF | ||
| + | |- | ||
| + | ! Notes | ||
| + | | -- | ||
| + | | -- | ||
| + | |- | ||
| + | |} | ||
Turn on the function generator with the power button in the bottom left corner. | Turn on the function generator with the power button in the bottom left corner. | ||
| Line 72: | Line 100: | ||
== Oscilloscope Measurements == | == Oscilloscope Measurements == | ||
| − | + | {|class="wikitable floatright" | |
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 20 Hz | ||
| + | | 20 Hz | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 0.5 V | ||
| + | | 0.5 V | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine | ||
| + | | Sine | ||
| + | |- | ||
| + | ! Notes | ||
| + | | -- | ||
| + | | -- | ||
| + | |- | ||
| + | |} | ||
Now you should be seeing something on the function generator's screen. Hurray! | Now you should be seeing something on the function generator's screen. Hurray! | ||
<ol> | <ol> | ||
| Line 94: | Line 145: | ||
| − | Create another | + | Create another copy of circuit 1 and Use channel 2 of the function generator to put an sine wave through the resistor (20Hz and 1V amplitude). Measure the voltage drop in the resistor using channel 2 of the oscilloscope and turn on the channel 2 display for the scope. |
<ol start="6"> | <ol start="6"> | ||
| Line 110: | Line 161: | ||
== More Function Generator Controls == | == More Function Generator Controls == | ||
| + | {|class="wikitable floatright" | ||
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 20 Hz || 20 Hz | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 0.5 V || 0.5 V | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine* || Sine | ||
| + | |- | ||
| + | ! Notes | ||
| + | | Will be adjusting <br> offset, phase || | ||
| + | |} | ||
| + | |||
| + | Your oscilloscope should be setup as in the end of the previous section: Channels 1 and 2 set to vertical 500mV scaling and 100ms horizontal scaling. Channel 1 should have a vertical offset of 0.5V and channel 2 should have a vertical offset of -0.5V. The scope should be reading the voltage across one resistor. Each resistor should be connected to one output of the function generator, as shown in circuit 1 above. | ||
<ol> | <ol> | ||
| Line 119: | Line 191: | ||
<li> Turn off and then back on channel 1 to get a random phase.</li> | <li> Turn off and then back on channel 1 to get a random phase.</li> | ||
<li> <b> Changing output phase</b>: Press the blue button under "Phase" on the function generator display. Use the knob and arrow buttons to adjust the phase of channel 1 so that the outputs of channel 1 and 2 look the same.</li> | <li> <b> Changing output phase</b>: Press the blue button under "Phase" on the function generator display. Use the knob and arrow buttons to adjust the phase of channel 1 so that the outputs of channel 1 and 2 look the same.</li> | ||
| − | <li> Move the phase back to 0 degrees.</li> | + | <li> Move the phase back to 0 degrees and align the phases.</li> |
| + | <li> Return the vertical offsets of channels 1 and 2 of the oscilloscope to 0V. You can do this simply by pressing in the vertical position knob.</li> | ||
| + | <li><b> Changing Oscilloscope Coupling</b>: Press the channel 1 button on the oscilloscope to open its menu. Changing the "Coupling" option from DC to AC. | ||
| + | <ul><li>What happened to the signal for channel 1?</li> | ||
| + | <li>Change the offset for channel 1 with the function generator. What happens to the scope signal for channel 1?</li> | ||
| + | <li>Set the offset of channel 1 to 0V and decrease the frequency, including trying some frequencies below 1Hz. What happens to the amplitude of the wave? Change the coupling of channel 1 back to DC. What happened to the amplitude now? | ||
| + | <li> What do you think the AC coupling mode is doing? How is reading the output wave? | ||
| + | <li> The AC coupling mode blocks the DC component of input signals and displays only the AC portion. So it effectively subtracts out the average value of a signal. Hopefully this is what you observe.</li> | ||
| + | <li> Change the output waveform of channel 1 to be a square wave. Adjust the horizontal scaling of the signal to get a clear look at the wave. What happened to it?</li> | ||
| + | <li> Square waves are made up of summing together sine waves of various frequencies (see the section below on Channel Comparisons). As you saw above, the AC coupling mode doesn't just get rid of the DC portion, but it also effects other low frequency components. Because the lower frequencies are modified, the signal for a square wave looks "wrong" in AC coupled mode.</li> | ||
| + | </ul> | ||
</ol> | </ol> | ||
== Oscilloscope Channel Comparisons == | == Oscilloscope Channel Comparisons == | ||
| − | + | {|class="wikitable floatright" | |
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 35 Hz* || 35 Hz | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 0.5 V || 0.5 V | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine* || Sine | ||
| + | |- | ||
| + | ! Notes | ||
| + | | Will be changing <br> phase || | ||
| + | |- | ||
| + | |} | ||
While performing experiments, just eyeballing the phase of two wave's isn't enough, there should be a better way to check it. | While performing experiments, just eyeballing the phase of two wave's isn't enough, there should be a better way to check it. | ||
| Line 150: | Line 251: | ||
<li> Turn on the channel 1 display and change the time basis to 20ms. Note that this changes the frequency spacing of the FFT greatly. Adjust the frequency basis back to 25Hz/div. You'll also note that the FFT graph looks "smoother". This is because the finest spacing in frequency that the FFT function can display is related to the full-time of the time signal - a shorter time means less fine spacing in frequency.</li> | <li> Turn on the channel 1 display and change the time basis to 20ms. Note that this changes the frequency spacing of the FFT greatly. Adjust the frequency basis back to 25Hz/div. You'll also note that the FFT graph looks "smoother". This is because the finest spacing in frequency that the FFT function can display is related to the full-time of the time signal - a shorter time means less fine spacing in frequency.</li> | ||
<li> Now what harmonics show up in the graph?</li> | <li> Now what harmonics show up in the graph?</li> | ||
| − | <li> Change the output of channel 1 to a "ramp". What does the channel 1 signal look like - is it a <i>triangle</i> wave or a <i>saw-tooth</i> wave? Which frequency components show in in this waveform?</li> | + | <li> Change the output of channel 1 to a "ramp". What does the channel 1 signal look like - is it a <i>triangle</i> wave or a <i>saw-tooth</i> wave? Which frequency components show in in this waveform?</li> |
| − | <li> <b> Setting Triangle/Saw-tooth Waves</b> On the function generator, press the blue button under the "Symm" label on the display. Symm sets how symmetric the ramp is. If " | + | <li> <b> Setting Triangle/Saw-tooth Waves</b> On the function generator, when using the ramp waveform, press the blue button under the "Symm" label on the display. Symm sets how symmetric the ramp is. If "Symm" is set to 50%, the function should be a triangle wave - 50% of the "front" half of the signal is the ramp. If "Symm" is 0%, 0% of the "front" half of the signal will be the ramp - that is the ramp will jump from its lowest value to its highest value, then slowly ramp back down to the lowest vale. If Symm is at 100%, the instantaneous jump will occur at the end of the wave. Both the 100% and the 0% Sym settings are saw-tooth waves. These three settings are shown below. |
| + | [[File:FuncGenRamp.png|x100px|thumb|center|Function Generator Ramp Output (none of which should be confused with the [https://commons.wikimedia.org/wiki/File:Nine_Inch_Nails_logo.svg Nine Inch Nails logo])]] | ||
| + | The Symm method for generating Triangle and Saw-tooth waves is not universal, but is described here in detail to familiarize you with the triangle and saw-tooth waveform. | ||
| + | </li> | ||
<li> Look both the triangle waves and the saw-tooth waves. How do their frequency components, the harmonic content of the wave, compare?</li> | <li> Look both the triangle waves and the saw-tooth waves. How do their frequency components, the harmonic content of the wave, compare?</li> | ||
</ul> | </ul> | ||
| Line 159: | Line 263: | ||
<li> Use the cursors to read out the heights of the first few harmonics of the saw-tooth wave. (try setting the vertical scale for the FFT plot to 50mVrms/div and the horizontal scale to 25Hz/div).</li> | <li> Use the cursors to read out the heights of the first few harmonics of the saw-tooth wave. (try setting the vertical scale for the FFT plot to 50mVrms/div and the horizontal scale to 25Hz/div).</li> | ||
<li> How do these heights compare? How do you think the coefficients, <math>A_k</math>, scale as a function of the harmonic, k, for the saw-tooth wave, based on your data? | <li> How do these heights compare? How do you think the coefficients, <math>A_k</math>, scale as a function of the harmonic, k, for the saw-tooth wave, based on your data? | ||
| − | <li> Try plotting your data | + | <li> Try plotting your data. Measured <math>A_k</math> vs <math>k</math> for a bunch of different points and plot it on a computer. Plot the data on a log-log plot and fit a line to this plot. The slope of that line, m, should be how the <math>A_k</math> coefficients scale with k, i.e. <math>A_k\propto k^m</math> .</li> |
<li> Change the waveform in channel 1 to be a triangle wave (Symm=50%). Measure the peak heights for the triangle wave. You may have to change the vertical or horizontal scaling to get better readings of the heights. How do the coefficients <math>A_k</math> scale for the triangle wave?</li> | <li> Change the waveform in channel 1 to be a triangle wave (Symm=50%). Measure the peak heights for the triangle wave. You may have to change the vertical or horizontal scaling to get better readings of the heights. How do the coefficients <math>A_k</math> scale for the triangle wave?</li> | ||
<li> Repeat for the sqaure wave.</li> | <li> Repeat for the sqaure wave.</li> | ||
| Line 166: | Line 270: | ||
</ol> | </ol> | ||
| − | == | + | == Frequency Sweep == |
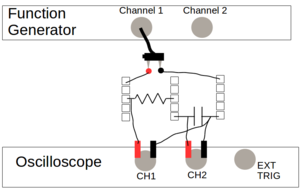
| − | [[File: | + | [[File:OscopeCir3.png|300px|right|thumbnail|<b> Circuit 2</b>: Circuit for Frequency Sweeping (Frequency Filter)]] |
| + | {|class="wikitable floatright" | ||
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 35 Hz* || -- | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 0.5 V || -- | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine || Off | ||
| + | |- | ||
| + | ! Notes | ||
| + | | Will be used in <br> Sweep Mode || -- | ||
| + | |- | ||
| + | |} | ||
| + | Connect the output of channel 1 across a resistor and the capacitor in series (so the current would flow through the resistor then through the capacitor). Measure the voltage across the resistor-capacitor pair on channel 1 of the oscilloscope. Measure the voltage across just the capacitor on channel 2 of the oscilloscope. This set up is a frequency filter - it allows some frequencies to pass through the pair while preventing other frequencies, or at least reducing their amplitudes significantly. | ||
| + | |||
| + | <ol> | ||
| + | <li> How do the amplitudes of the waves on the oscilloscope compare? Change the frequency of channel 1 by a lot. How does the amplitude change? Do you think high or low frequencies can get through (you should have studied a similar circuit when following the [[Multimeters]] module.</li> | ||
| + | <li> This would be much easier to study if we could look at multiple frequencies in quick succession. So let's do that.</li> | ||
| + | <li> <b> Frequency Sweep</b>: Press the "Sweep" Button on the function generator (while controlling the output of channel 1). This mode will continually change the output frequency of the generator, allowing us to analyze what happens as the frequency changes. | ||
| + | <ul> | ||
| + | <li> Press the button under the "Start" label and set the frequency to 100Hz</li> | ||
| + | <li> Press the button under the "Stop" label and set the frequency to 300Hz.</li> | ||
| + | <li> Press the button under the "Time" label and set the time to 1sec.</li> | ||
| + | <li> The function generator is now set up to constantly (linearly) change the frequency from 100Hz to 300Hz in 1sec. Adjust the horizontal axis on the scope to be 5ms/division. Observe how the waveform changes.</li> | ||
| + | <li> If you change the direction of the sweep (starting at 300Hz and stopping at 100Hz), how do you think the waveform on the scope will change? Try it. | ||
| + | </ul> | ||
| + | <li> Change the scope's trigger to be on channel 2. Adjust the level of the trigger to be around +400mV. Change the sweep's start to 300Hz and end to 65kHz. Yes, that's kilohertz. Adjust the horizontal scale on the function generator to be 100ms/division.</li> | ||
| + | <li><b>Trigger Position</b>: Turn the horizontal position knob to move the location of the trigger. Normally, the trigger "starts" at the center of the screen (marked with a pentagon with a "T" in it). Move the trigger to the far left side of the screen. You can now see more of the trace that occurs after the trigger occurs.</li> | ||
| + | <li>What are you observing on the screen? Does this information tell you if the filter we've built is low-pass or high pass? </li> | ||
| + | <li> Why do you think you changed the trigger level?</li> | ||
| + | <li> What do you think would happen if you flip the start and stop points of the sweep? Try it.</li> | ||
| + | <li> <b> Sweep Scaling</b>: Press the button under the "Linear" label. Press it again until it changes to "Log." This changes the sweep so that it does not change linearly but logarithmically. This is convenient if you'd like to observe how the circuit responds over several orders of magnitude in frequency.</li> | ||
| + | <li> Change the sweep to go between 10Hz and 80Hz. Change the horizontal axis on the scope to be 50ms.</li> | ||
| + | <li> <b>Roll Time Basis</b>: Open the horizontal menu on the scope and change the Time Base to Roll. Rather than displaying a full wave form then erasing it to display new data, this mode rolls the data over the screen as it goes. Change between the linear and logarithmic mode for the sweep and see how the form changes as it rolls. | ||
| + | <ul><li> The roll time basis might be useful for times when you are attempting to minimize/maximize a signal. It will give you a "live" update on what the signal is, while still showing you what the signal was in the recent past.</li></ul> | ||
| + | </ol> | ||
| + | |||
| + | == X-Y Plotting and External Trigger == | ||
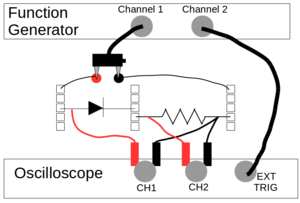
| + | [[File:OscopeCir2.png|300px|right|thumbnail|<b>Circuit 3</b>: Circuit for X-Y Plotting (Diode + Resistor)]] | ||
| + | {|class="wikitable floatright" | ||
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 35 Hz || 35 Hz | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 1.5 V || 1.5 V | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine || Square | ||
| + | |- | ||
| + | ! Notes | ||
| + | | Sync Phases || Used as External <br> Trigger to scope | ||
| + | |- | ||
| + | |} | ||
Disconnect the two resistors from the function generator. With channel 1, output a sine wave with frequency of 35Hz and amplitude of 1.5V. Connect the output of channel 1 to the diode and one resistor in series. Use the channel 1 of the oscilloscope to measure the voltage across the diode-resistor pair and channel 2 to measure the voltage across just the resistor. These should be set up like the diagram to the right. | Disconnect the two resistors from the function generator. With channel 1, output a sine wave with frequency of 35Hz and amplitude of 1.5V. Connect the output of channel 1 to the diode and one resistor in series. Use the channel 1 of the oscilloscope to measure the voltage across the diode-resistor pair and channel 2 to measure the voltage across just the resistor. These should be set up like the diagram to the right. | ||
| Line 175: | Line 345: | ||
<ol> | <ol> | ||
<li> <b> External triggering</b>: Connect the output of channel 2 of the function generator to the External Trigger input of the oscilloscope. In the oscilloscope's trigger menu, set the source to External, Edge triggered, and a down arrow for the direction. | <li> <b> External triggering</b>: Connect the output of channel 2 of the function generator to the External Trigger input of the oscilloscope. In the oscilloscope's trigger menu, set the source to External, Edge triggered, and a down arrow for the direction. | ||
| − | <ul><li> The external triggering allows you to trigger the scope's data recording without interfering with displaying two different voltage signals.</li> | + | <ul><li> The external triggering allows you to trigger the scope's data recording without interfering with displaying two different voltage signals. This is useful, for example, when measuring the voltage across a resistor and a capacitor in an RC circuit as there will be a phase different between the voltages. </li> |
| − | <li> The edge triggering is best for square pulses as it just relies on the signal going from high-to-low (or low-to-high). For non-square waves, this will behave identically to the slope triggering, but not vice-versa.</li> | + | <li> The edge triggering is best for square pulses as it just relies on the signal going from high-to-low (or low-to-high). Using the slope setting for square waves cause issues as the slope when a square wave changes is infinite. For non-square waves, this will behave identically to the slope triggering, but not vice-versa.</li> |
</ul> | </ul> | ||
<li> Set the vertical scale of both oscilloscope channels to 500mV and the horizontal scale to 5ms. How do the two graphs of the voltage out of the function generator (channel 1) and the voltage dropped across the resistor compare (channel 2) compare?</li> | <li> Set the vertical scale of both oscilloscope channels to 500mV and the horizontal scale to 5ms. How do the two graphs of the voltage out of the function generator (channel 1) and the voltage dropped across the resistor compare (channel 2) compare?</li> | ||
| Line 183: | Line 353: | ||
<ul><li>Set the "Cursor A" control to CH2 and move the cursor to the "corner" where the voltage turns on or off. You can eye-ball it, or move watch the "A->Y" chart value goes above 0V. </li> | <ul><li>Set the "Cursor A" control to CH2 and move the cursor to the "corner" where the voltage turns on or off. You can eye-ball it, or move watch the "A->Y" chart value goes above 0V. </li> | ||
<li> Set the "Cursor B" control to CH1 and move this cursor so that the "|ΔX|" value in the chart is 0s. Here, the time-separation between the two cursors is zero.</li> | <li> Set the "Cursor B" control to CH1 and move this cursor so that the "|ΔX|" value in the chart is 0s. Here, the time-separation between the two cursors is zero.</li> | ||
| − | <li> What is the voltage read at cursor B (the "B-> | + | <li> What is the voltage read at cursor B (the "B-> Y" value in the chart)? This is the minimum voltage needed for current to flow through the resistor.</li> |
| + | </ul> | ||
| + | <li> <b> X-Y Time Basis</b>: Press the "Menu" button in the middle of the horizontal control column. Use the menu buttons to change the "Time Base" from Y-T to X-Y. This shows the voltage in channel 1 plotted along the x-axis and the voltage in channel 2 plotted along the y-axis. | ||
| + | <ul><li>You'll note that the cursor menu changes from track mode - while using the X-Y time basis, you cannot use track mode.</li> | ||
| + | <li> <b>Adjusting Horizontal Axis in X-Y Basis</b>: Using the horizontal adjustment knobs does not change the horizontal axis in the X-Y basis. To do this, press the channel 1 button to open the channel 1 adjustment menu. Use the vertical adjustment knobs to change the scale/center of the voltage for channel 1 - and hence the horizontal axis in the X-Y basis. </li> | ||
| + | <li> <b> Adjusting Vertical Axis in X-Y Basis</b>: Open the channel 2 adjustment menu. Use the vertical adjustment knobs to change the scale/center of the voltage for channel 2 - and hence the vertical axis in the X-Y basis.</li> | ||
| + | <li> Adjust the axes so as much of the graph shows up on the oscilloscope.</li> | ||
| + | <li> <b> Sampling in the X-Y basis</b>: The graph for the X-Y mode will probably be "moving around". This is due to a mismatch between the oscillation frequency and the sampling rate of the oscilloscope. You can use the horizontal scale knob to adjust the sampling rate until you can see the entire range of the data you are plotting.</li> | ||
| + | </ul> | ||
| + | <li> Use vertical cursors find the input voltage (channel 1 voltage) that causes current to start to flow through the diode and to the resistor. Estimate the voltage at which the out voltage follows ohm's law through the resistor. This is the "forward" voltage for the diode. Does your measured value agree with the value from the [[https://www.fairchildsemi.com/datasheets/1N/1N914.pdf diode's data sheet]]. | ||
| + | </ol> | ||
| + | |||
| + | == Noise and Averaging == | ||
| + | |||
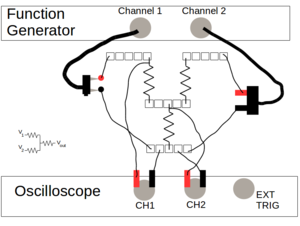
| + | [[File:OscopeCir4.png|300px|right|thumbnail|<b>Circuit 4</b>: Circuit for Noise and Averaging (Poor Voltage Summer)]] | ||
| + | {|class="wikitable floatright" | ||
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 35 Hz || 35 Hz* | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 0.5 V || 0.5 V | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine || Noise* | ||
| + | |- | ||
| + | ! Notes | ||
| + | | -- || -- | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | Build the following circuit: Connect the positive (red) outputs of both channels to one end of different resistors (resistors 1 and 2). The other end of each resistor should be connected to one end of a third resistor (one end of all three resistors should touch). Connect the black outputs of both channels to free end of the third resistor (resistor 3). This circuit is shown to the right, along with a simplified "standard" circuit drawing. | ||
| + | |||
| + | This is a (crude) voltage summer: the voltages from the two output channels will add together in the third resistor. This is not a very good voltage summer, as the output voltage in the third resistor isn't just the sum, but sum of the two voltages each scaled by some factor (related to the resistances). There are much better ways to sum voltages, but this will work fine for our purposes. | ||
| + | |||
| + | Connect the input of channel 1 of the oscilloscope to the voltage across resistor 1 and the input of channel 2 of the oscilloscope to the voltage across resistor 3. Set the scope to trigger on channel 1 and set the horizontal scale so that a few wave forms show on the display. Adjust the vertical scales of each channel as you feel appropriate. | ||
| + | |||
| + | <ol> | ||
| + | <li> Have both channels output sine waves and align the phases of the function generator output.</li> | ||
| + | <li> How does the signal in channel 2 (the sum(ish) of the two signals) compare when you adjust the phase of channel 2?</li> | ||
| + | <li> <b> Noise Generation</B>: Select channel 2 control on the function generator and press the "Noise" button. This will generate a random noise-y signal output. Note which wave properties you can change while in noise mode.</li> | ||
| + | <li> Observe the voltage across resistor 2 on channel 2 oscilloscope, see how noisy it is?</li> | ||
| + | <li> Return the output of channel 2 to measure the voltage across resistor 3.</li> | ||
| + | <li> Adjust the amplitude of the noise signal and note how the summed signal changes on the oscilloscope. Return the amplitude to 0.5V.</li> | ||
| + | <li> <b>Averaging Signals</b>: Press the "Acquire" button on the oscilloscope. Change the "Acquisition" item in the menu to "Average". | ||
| + | <ul> <li> This setting displays the average of the previous N scope traces (N is set in the "Averages" menu item that appears). Each time you change any setting on the scope, the average must be recalculated. | ||
| + | <li> Adjust the number of averages and observe how the signal changes. Set the number of averages to 4.</li> | ||
| + | <li> Change the amplitude of the sine wave of channel 1 to 1.0V. Note how long it takes for the signal to "adjust" on the oscilloscope. Repeat this with the number of averages set to 32. How does the time for the signal to "adjust" compare to setting the averages to 4?</li> | ||
| + | </ul> | ||
| + | </li> | ||
| + | <li> Return the acquisition mode to normal. | ||
| + | <li> Try changing the amplitude of the noise signal in channel 1. What happens to the summed (and averaged) signal. Why do you think this would happen?</li> | ||
| + | <li> Display the fourier transform of channel 2 on the oscilloscope. Adjust the amplitudes of both channels of the function generator and observe changes in the 35Hz peak. Repeat this after turning on signal averaging.</li> | ||
| + | </ol> | ||
| + | |||
| + | == Oscilloscope Time Properties== | ||
| + | {|class="wikitable floatright" | ||
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 50 Hz* || 50 Hz | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 0.5 V || 0.5 V | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine || Sine | ||
| + | |- | ||
| + | ! Notes | ||
| + | | -- ||-- | ||
| + | |} | ||
| + | |||
| + | Construction 2 copies of circuit 1, one for each output of the function generator. Use scope channel 1 to read the voltage output from channel 1 of the oscilloscope. Use scope channel 2 to read the voltage output from channel 2 of the oscilloscope. | ||
| + | |||
| + | <ol> | ||
| + | <li> <b> Oscilloscope Sample Rate</b>: Open the horizontal menu on the oscilloscope. Change the horizontal scale to 10ms. Note that as you change the time, the "Sa Rate" menu item changes. This tells you the sample rate of the oscilloscope - how many voltages it saves every second. Note that as you go to shorter times, the scope must record MORE samples do account for the fine time resolution you are asking it to display.</li> | ||
| + | <li> Set the time scaling to 10ms.</li> | ||
| + | <li> On a piece of paper, draw five complete sine waves. | ||
| + | <ul> <li>Let's say that this wave is recorded by the oscilloscope at a rate equal to its frequency - that is for every each complete wave, the oscilloscope records ONE data point. On your wave, put an x at each recorded data point - make sure these data points are equally spaced horizontally. </li> | ||
| + | <li> Draw a curve connecting these data points - this is the plot that the oscilloscope would show you.</li> | ||
| + | <li> How similar is this plot to the actual wave you drew?</li> | ||
| + | <li> Repeat the steps using a sampling rate that is a half and twice the frequency of your drawn wave (1 data point recorded for every 2 complete waves and 2 data points recorded for every complete wave).</li> | ||
| + | <li> What can you conclude about the above? How should the sample rate of your oscilloscope compare to the frequency of your signal such that you get a reliable trace on the scope? </li> | ||
| + | <li> What you've drawn and discovered is called <i>aliasing</i>, no let's observe it with the scope.</li> | ||
</ul> | </ul> | ||
| − | <li> < | + | <li> With 10ms scaling, what is the sample rate of your scope? Make sure the scope is triggered on channel 2 and change the frequency of channel 1 to the match the sample rate. Does the scope display a similar graph to what you've drawn?</li> |
| + | <li> Set the frequency to twice your sample rate (so that the sample rate is half the frequency). What does the graph look like? Does this agree with what you drew?</li> | ||
| + | <li> Set the frequency to half your sample rate (so the sample rate is twice the frequency). What does the graph look like? Does this agree with what you drew? (The frequency should be really large, so that many, many completed waves should appear on the screen - they should all merge together and just look like a thick band).</li> | ||
| + | <li> Why do the graphs on the oscilloscope change, rather than just stay stationary?</li> | ||
</ol> | </ol> | ||
| − | Function Generator | + | |
| + | == Termination == | ||
| + | [[File:OscopeCir5.png|300px|right|thumbnail|<b>Circuit 5</b>: Circuit for Termination (Voltage Divider)]] | ||
| + | {|class="wikitable floatright" | ||
| + | |+ Base Function Generator Settings | ||
| + | |- | ||
| + | ! | ||
| + | ! Channel 1 | ||
| + | ! Channel 2 | ||
| + | |- | ||
| + | ! Frequency | ||
| + | | 20 Hz || -- | ||
| + | |- | ||
| + | ! Amplitude | ||
| + | | 0.5 V || -- | ||
| + | |- | ||
| + | ! Shape | ||
| + | | Sine || OFF | ||
| + | |- | ||
| + | ! Notes | ||
| + | | -- ||-- | ||
| + | |} | ||
| + | |||
| + | Build the circuit to the right - a voltage divider. The input voltage (from the function generator) is split between the two resistors (relative to their resistances). When the resistors are the same resistance, the voltage dropped across each resistor is half the input resistance. More specifically, the resistance across the 2nd resistor is | ||
| + | <br><math>V_2=\frac{R_2}{R_2+R_1}V_0</math> | ||
| + | |||
| + | <ol> | ||
| + | <li> Test the above equation by comparing the input voltage (<math>V_0</math>, voltage across both resistors) and the voltage across the 2nd resistor. Use horizontal cursors to check the voltages on each channel.</li> | ||
| + | <li> <b>Measurement Menu</b>: Press the "Measure" button on the screen. This menu gives a large variety of voltage and time measurement options for a channel. It will display the measured results at the bottom of the screen. | ||
<ul> | <ul> | ||
| − | <li> | + | <li>Set the source to Channel 1. </li> |
| − | <li> | + | <li>Press the voltage button and navigate the menu to select "Vamp". To move the cursor, use the selection knob and you can select an option either by pressing the knob in or by pressing the button next to Voltage again. A measurement value should appear on the bottom of the screen and will tell you the amplitude of the measured signal (in this case the amplitude is defined to be the peak-to-peak voltage of the sine wave).</li> |
| − | <li> | + | <li>Change the source to channel 2 and display the peak-to-peak voltage for channel 2.</li> |
| + | <li> How do these amplitudes compare? Do they agree with the equation above, assuming the resistances of the resistors are (almost) equal.</li> | ||
| + | <li> The "clear" button will remove the measurements from the screen, although you should keep the measurement values on the screen for now.</li> | ||
</ul> | </ul> | ||
| + | <li> <b>Terminator</b>: Add a voltage terminator between the BNC-to-banana-plug adapter and the input of channel 2 of the oscilloscope. Set the termination resistance to 50ohms. | ||
| + | <li> What happens to the amplitude to the voltage in channel 1? If the measured amplitude changes to a series of asterisks you'll have to change the vertical scale for channel 1 in order to measure the amplitude.</li> | ||
| + | <li> Change the termination resistance. How does the measured voltage change? Does the measured voltage get closer to what you expect (from the equation above) when the terminator's resistance gets larger or smaller?</li> | ||
| + | <li> The oscilloscope has an input resistance, that is there is a resistor connecting the positive and negative inputs of each channel of the oscilloscope. What is that resistance (it can be read from the front of the oscilloscope)? With your answer from the previous question, does this lead you to trust the voltage readings of the oscilloscope without a terminator?</li> | ||
| + | <li> The termination resistance (or the input resistance of the oscilloscope) and the 2nd resistor in the voltage divider are acting in parallel, such that the termination resistance is acting as a <i>load</i> on the voltage divider - that is some extra electrical component that the voltage divider is supplying voltage for. The effective resistance of the two resistors in parallel is <math>R'=\frac{R_2 R_{term}}{R_2+R_{term}}</math>. | ||
| + | <ul><li>For a very small termination resistance (<math>R_{term} << R_2</math>), how does the effective resistance, <math>R'</math> compare to the two resistances, <math>R_2</math> and <math>R_{term}</math>? How would <math>R_{term}</math> affect the voltage across resistor 2 above?</li> | ||
| + | <li>If the termination resistance is much larger than the resistance of resistor 2 (<math>R_{term} >> R_2</math>), how does the effective resistance,<math>R'</math> compare to the two resistances, <math>R_2</math> and <math>R_{term}</math>? How would <math>R_{term}</math> affect the voltage across resistor 2 above?</li> | ||
| + | <li> For using the oscilloscope to measure voltages in a circuit, do you think having a larger or smaller termination voltage would be preferred? Why?</li> | ||
| + | </ul> | ||
| + | There are ways to prevent loads from affecting the behavior of voltage dividers. See the Electronics Obstacle Course section on [http://hank.uoregon.edu/wiki/index.php/Electronics_Obstacle_Course#Instrumentation_and_Loading Instrumentation and Loading] for more information.</li> | ||
| + | <li> To look at the effects of the terminator more carefully, let's remove the voltage divider entirely: connect the output of channel 1 of the function generator to the terminator and then directly to the oscilloscope.</li> | ||
| + | <li> The function generator output also has a resistance between the positive and negative outputs of each channel. What is this resistance (it is on the front of the function generator)?</li> | ||
| + | <li> Set the resistance of the terminator to match the resistance of the function generator. How does the amplitude of the wave measured on the oscilloscope compare to the amplitude that you have set on the function generator? </li> | ||
| + | <li> The matched resistances (output of function generator and input of oscilloscope) are acting as a voltage divider. According to the equation above, are you measuring what you expect with the oscilloscope?</li> | ||
| + | <li> Matching the resistances is called <b>impedance matching</b> (recall that impedance is sort of a generalized resistance for resistors, capacitors, and inductors). Impedance matching is important for carefully measuring signals - especially those that are oscillating. | ||
| + | <ul><li> Similar to when light enters a medium with a different index of refraction, when electric waves in a wire reaches an object with a different impedance the wave can partially reflect backwards down the wire. </li> | ||
| + | <li> If an electrical signal is traveling between two objects with different impedances, the signal can repeatedly reflect from each object, seriously impacting the signal seen by each object. </li> | ||
| + | <li> Impedance matching avoids this problem, but as a result, divides the measured voltage in half. For this reason, terminators are often labeled with having "3dB attenuation" as halving a signal is a 3 decibel decrease (review wikipedia's article on [https://en.wikipedia.org/wiki/Decibel decibels]).</li> | ||
| + | <li> For example, individual photons can be measured by many devices, including an Avalanche Photo-Diode (APD). These will convert a photon it sees into a very short (nanosecond long) electric pulse. Counting these pulses with a device that is not properly impedance matched to the APD can result in photon counts that are too high - a portion of the electron pulse is reflected back to the APD, then back towards the counting device and counted a 2nd time. This can repeat a number of times, giving photon counts that are much higher than are actually being detected. | ||
| + | </ul> | ||
| + | <li> Often, oscilloscopes have settings that can change the input impedance of the oscilloscope (note that the oscilloscope you are using does not). This allows you to easily set up the scope for making appropriate measurements.</li> | ||
| + | </ol> | ||
| − | + | ||
| + | == Exporting Data== | ||
| + | With the function generator, sine wave with an amplitude of 0.8V and frequency 715 Hz. Use the measure menu to display the RMS voltage of the signal from the function generator. Record a single trace of this wave on the oscilloscope, showing at least 12 complete waves. | ||
| + | |||
| + | <ol> | ||
| + | <li> <b>Exporting Data</b> Insert a USB storage device into the USB slot on the front of the oscilloscope. | ||
| + | <ul> | ||
| + | <li>Press the Storage button and change the storage menu item to CSV.</li> | ||
| + | <li> Set the Data Depth to Displayed.</li> | ||
| + | <li> Press the blue menu button next to "External". This will open a menu that should show you to file system of the USB drive. Use the menu buttons to change to whatever location on the drive you would like and then press the Save button. You can name the file whatever you'd like.</li> | ||
| + | <li> Press the back button (arrow at the bottom of the menu) until you return to the storage menu's top level. Change the data depth to Maximum and save the data again (as a different file name than before, of course). | ||
| + | <li> After the file is done saving, you can remove the USB device.</li> | ||
| + | </ul> | ||
| + | <li>Plug the USB device into a computer. Open the two CSV files with a text document reader (not a spreadsheet program). How is the data saved? Is the data saved as tab- or comma-deliminated (tabs or commas separate columns).</li> | ||
| + | <li> Open the files in a spreadsheet program (LibreOffice Calc is available on the computers in the advanced projects lab). When the program asks about importing data, make sure that the correct delimination is selected.</li> | ||
| + | <li> Plot the two sets of data as X-Y scatter plots. What is the difference between the "Displayed" (first file saved) and the "Maximum" data depth options?</li> | ||
| + | <li> Calculate the RMS voltage of the data. | ||
<ul> | <ul> | ||
| − | <li> | + | <li> In LibreOffice Calc, you can use the functions sumsq(), sqrt(), and count() to calculate the RMS voltage. sumsq() calculates the sum of the squares of the data points given, count() gives the number of non-empty cells in the defined region, and sqrt() calculates the square root of its input. </li> |
| − | + | <li>Does this agree with the RMS voltage given by the oscilloscope? </li> | |
| − | + | <li>How does it compare to the amplitude of the sine wave? Try dividing by the value you set the amplitude to.</li> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | <li> | ||
| − | |||
| − | <li> | ||
</ul> | </ul> | ||
| + | </ol> | ||
Latest revision as of 12:35, 19 January 2022
Function generators and oscilloscopes will be covered as a pair. Oscilloscopes measures voltages as a function of time and displays the data on a graph. Function generators create a changing voltage under some function of time (often it is a sine wave, although there are a number of other shapes we'll see below). Thus, these two are natural to pair together. Note that sometimes oscilloscope is shortened to "oscope" or just "scope".
This module will also review some circuit elements (diode operation), fourier analysis of a signal and data fitting to a function.
Each section has a table describing the function generator output setup for that section. Controls marked with an asterisk will be changed during that section.
This module is part of the General Lab Equipment Obstacle Course.
Contents
- 1 Equipment
- 2 Circuit Setup
- 3 Oscilloscope Setup
- 4 Function Generator Setup
- 5 Oscilloscope Measurements
- 6 More Function Generator Controls
- 7 Oscilloscope Channel Comparisons
- 8 Frequency Sweep
- 9 X-Y Plotting and External Trigger
- 10 Noise and Averaging
- 11 Oscilloscope Time Properties
- 12 Termination
- 13 Exporting Data
Equipment
For this topic, you'll need the following equipment:
- Rigol DG1022 Function Generator
- Rigol DS1102E Digital Oscilloscope
- 1kohm resistor
- 1uF capactitor
- 1N4148 Diode
- Protoboard
- A number of short wires
- A few BNC-to-banana socket adapters (left adapter shown to right)
- BNC-to-banana plug adapter (right adapter shown to right)
- Three BNC cables
- Two full sets of alligator clip - banana plug cables (that is a total of four cables with alligator clips on one end and banana plugs on the other)
Circuit Setup
We will need some circuit to read voltages from. Setup a circuit to run the output voltage of the function generator through your resistor and read the voltage dropped across the resistor with the oscilloscope. How to carefully set this up follows.
To bottom output of the function generator, plug in the BNC and attach the free end to the BNC-to-banana-plug adapter. The plastic cap on the banana-socket should unscrew slightly and reveal a hole underneath. For each socket, push the exposed end of a wire through the hole, then tighten down the cap to secure the wire to the socket. The wires should not go to the same row of holes in the protoboard. Connect the wire to a row on the protoboard, and plug the adapter into the sockets. The rows into which you plugged the wires should now be connected to the output of the function generator. Plug opposite ends of the resistor into the two rows of the protoboard that you have powered. Current that flows from the function generator should now travel through the resistor.
On each side of the resistor, attach an alligator clip. Attach a BNC-to-aligator-socket adapter to channel 1 of the oscilloscope. Plug the ends of the alligator clip into the banana-sockets. This should allow the oscilloscope to display, on channel 1, the voltage across the resistor, as shown to the right.
Oscilloscope Setup
Turn on the oscilloscope with the button on the top of it.
- Controlling Displayed Inputs: Using the CH1, CH2, MATH, and REF buttons on the right side of the display, press each one until only the CH1 button is lit. This will allow the oscilloscope to ONLY display the input from the first channel.
- Changing Vertical Scale: Using the bottom knob in the "Vertical" column of controls, turn it until the yellow numbers in the bottom left corner of the screen read "200mV". This sets the oscilloscope such that the vertical scale has 200mV of measured voltage between each of the horizontal lines.
- What is the voltage at the top and bottom of the graph?
- Changing Horizontal (time) Scale: Turn the knob at the bottom of the "horizontal" column of controls. Turn it until the white "Time" setting at the bottom of the screen reads 50.00ms. This sets the bottom (time) axis so there are 50ms of data between vertical lines on the graph.
- What is the full amount of of time displayed on the display?
- Changing Trigger Source: It is likely that nothing is happening on the screen. Press the "MENU" button in the "Trigger" column of controls. A display should appear on the screen. Press the button next to the "Source" setting until it highlights "AC LINE'. You can also use the dial at the top of the controls to change which selection is made. Change the "Slope" setting to the arrow pointing upwards.
- The "Trigger" control tells the oscilloscope when to update data. The scope is constantly recording data, but only displays it when it is triggered. It is triggered when the source's voltage (currently the voltage in the AC line) crosses 0 volts in the direction set up by the slope (currently going from below 0V to above 0V. When it is triggered, the scope fills the left half of the screen with the data it has been recording, then fills the right half in real time.
- One being triggered, the oscilloscope will record data for the entire length of time the window is set for (with the horizontal time control knob - see step 3, above).
- You should be seeing the line on the display change. How long does it take for the line to change? How does this compare to the length of the x-axis (full time of the data).
- After it finishes recorded data, it will wait for another trigger. Once it sees the new trigger, it will overwrite the data it has displayed, so you should be seeing the line update roughly every 0.6s.
- Try changing the time-axis to 500ms. See how the scope updates? be sure to set things back to 50ms before continuing.
- Press the white circular "Menu On/Off" just to the right of the display. This should turn off any menus and show you the full screen of data.
A yellow line of 0 volts is boring, so let's give the oscilloscope a signal to measure.
Function Generator Setup
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 20 Hz | -- |
| Amplitude | 0.5 V | -- |
| Shape | Sine | OFF |
| Notes | -- | -- |
Turn on the function generator with the power button in the bottom left corner.
- Changing Output Controls: Press the "CH1|CH2" button under the display until the left box turns black, this gives you control over the output of channel 1.
- Changing Output waveforms: Press the "Sine" button under the function generator display to create a sine wave. The display should read "Sine" in the top left corner and the image of a sine wave should appear under it.
- Controlling Frequency: Press the left most blue button on the until the label above it reads "Freq". This allows you to set the frequency of the box. Using the two arrow buttons under the function generator dial and the dial itself to set the output frequency to 20Hz.
- Controlling Amplitude: Press the 2nd (from the left) blue button under the display so that the label above it reads "Ampl". This gives you control of the amplitude of the wave. The function generator has you input the wave's peak-to-peak voltage, that is the total voltage between the tops of the waves and the bottoms.
- If the sine wave is y=A Sin( 2 pi f t), how does the peak-to-peak voltage compare to the amplitude, A, of the wave?
- Turning on/off output: Press the bottom output button on the right side of the function generator to turn on channel 1 of the function generator. The label in the top-right corner of the left box on the display should change to "ON" from "OFF".
Oscilloscope Measurements
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 20 Hz | 20 Hz |
| Amplitude | 0.5 V | 0.5 V |
| Shape | Sine | Sine |
| Notes | -- | -- |
Now you should be seeing something on the function generator's screen. Hurray!
- If each horizontal line on the screen is 200mV, about what does the oscilloscope read for the amplitude of the wave. Is this correct?
- Count the number of full waves on the display. This is challenging yes? There are (at least) two ways to deal with this.
- Recording Single Scope Traces: Press the green-glowing RUN/STOP button in the top right corner of the oscilloscope. It should turn red and once the oscope completes its current run of recording data, it will stop recording data and keep the data saved on the screen. Pressing the RUN/STOP button again will return to recording data normally.
- The better way to look at the data is by changing the Triggering Source of the scope. Change the trigger source to Channel 1. Now the data only updates when it is triggered by channel 1.
- Because the scope is triggered when channel 1 crosses from negative to positive voltage, the exact center of the graph should be at 0V.
- Predict how the graph will change if you change the triggering slope to the down-arrow.
- Now change the slope to the down arrow. Was your prediction correct?
- Put the trigger slope back to the up-arrow.
- Changing Trigger Level: You can change the trigger so that it happens not when the voltage crosses zero, but when it crosses any arbitrary voltage level. To do this, turn the top knob in the "Trigger" control column. An orange line, with an arrow labeled "T" to the left of the graph, should appear and follow how you turn the knob. This sets the voltage at which the scope is triggered. When the voltage crosses this threshold (in the direction chosen with "slope") the oscope will begin collecting data.
- As you change the triggering voltage, how does the voltage at the left side of the screen change? Does this make sense?
- Predict what will happen if you move the trigger voltage above (or below) the amplitude of the wave. Try it. Return the trigger voltage to 0V.
- Change the scale of the vertical axis to 100mV. Did the graph do as you'd expect?
Create another copy of circuit 1 and Use channel 2 of the function generator to put an sine wave through the resistor (20Hz and 1V amplitude). Measure the voltage drop in the resistor using channel 2 of the oscilloscope and turn on the channel 2 display for the scope.
- Controlling Multiple Scope Input Channels: Pressing the CH1 button on the scope will give you control over channel 1. Set its vertical scale to 500mV. Pressing the CH2 button will then give you control over channel 2's properties. Set its vertical scale to 500mV. The two graphs should line up on top of each other.
- Change the horizontal scale of Channel 1 to 50ms.
- Change the horizontal scale of Channel 2 to 100ms.
- What happened to the scale of Channel 1?
- Set both horizontal scales to 100ms.
- Controlling 0V point of graph: Turning the top knob on the vertical column of controls will adjust the offset of the scope. Change the offset of channel 1 to +0.5V and the offset of channel 2 to -0.5V.
- Set the scope to trigger on Channel 2 when it crosses 0V.
You should now see two identical traces on the scope, with their traces offset from each other by 1V.
More Function Generator Controls
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 20 Hz | 20 Hz |
| Amplitude | 0.5 V | 0.5 V |
| Shape | Sine* | Sine |
| Notes | Will be adjusting offset, phase |
Your oscilloscope should be setup as in the end of the previous section: Channels 1 and 2 set to vertical 500mV scaling and 100ms horizontal scaling. Channel 1 should have a vertical offset of 0.5V and channel 2 should have a vertical offset of -0.5V. The scope should be reading the voltage across one resistor. Each resistor should be connected to one output of the function generator, as shown in circuit 1 above.
- Setting Output Waveforms: Make sure you are controlling the output of Channel 1 of the function generator. Press some of the other waveform buttons (Square, ramp, pulse) under the display and observe the changes on the oscilloscope.
- Return the wave form to be a sine wave. We want to overlap the two signals on the oscilloscope by adjusting the voltage output from channel 1 of the function generator, that is we want the voltage to be V=V0+A sin(2 pi f t). By how much should you adjust the voltage by to make this happen?
- Changing Wave Offset: Press the button under the "Offset" label on the display. Use the knob and arrows on the function generator to change the voltage and make the two graphs overlap.
- It is likely that your graphs will not overlap perfectly. They'll have some phase difference between them. The phase of each output is set randomly when that channel of the function generator is turned on. See that by turning on and off the output of channel 1 a few times. Note that the wave forms shift relative to eachother.
- Aligning output phase: Press the blue button under the "AligPha" label on the display. This should fix both phases so that they are the same. Did it?
- Turn off and then back on channel 1 to get a random phase.
- Changing output phase: Press the blue button under "Phase" on the function generator display. Use the knob and arrow buttons to adjust the phase of channel 1 so that the outputs of channel 1 and 2 look the same.
- Move the phase back to 0 degrees and align the phases.
- Return the vertical offsets of channels 1 and 2 of the oscilloscope to 0V. You can do this simply by pressing in the vertical position knob.
- Changing Oscilloscope Coupling: Press the channel 1 button on the oscilloscope to open its menu. Changing the "Coupling" option from DC to AC.
- What happened to the signal for channel 1?
- Change the offset for channel 1 with the function generator. What happens to the scope signal for channel 1?
- Set the offset of channel 1 to 0V and decrease the frequency, including trying some frequencies below 1Hz. What happens to the amplitude of the wave? Change the coupling of channel 1 back to DC. What happened to the amplitude now?
- What do you think the AC coupling mode is doing? How is reading the output wave?
- The AC coupling mode blocks the DC component of input signals and displays only the AC portion. So it effectively subtracts out the average value of a signal. Hopefully this is what you observe.
- Change the output waveform of channel 1 to be a square wave. Adjust the horizontal scaling of the signal to get a clear look at the wave. What happened to it?
- Square waves are made up of summing together sine waves of various frequencies (see the section below on Channel Comparisons). As you saw above, the AC coupling mode doesn't just get rid of the DC portion, but it also effects other low frequency components. Because the lower frequencies are modified, the signal for a square wave looks "wrong" in AC coupled mode.
Oscilloscope Channel Comparisons
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 35 Hz* | 35 Hz |
| Amplitude | 0.5 V | 0.5 V |
| Shape | Sine* | Sine |
| Notes | Will be changing phase |
While performing experiments, just eyeballing the phase of two wave's isn't enough, there should be a better way to check it.
- Signal Difference: Press the "MATH" button on the oscilloscope. A purple graph should appear. Use the blue menu buttons and dial to set the "Operate" menu to "A-B", Source A to CH1 and Source B to CH2. Thus, the purple menu should be the difference between the two channels. Adjust the vertical scale of the function generator to 20mV.
- Change the phase of channel 1 with the function generator to make the difference signal as small as you can make it, changing the scale and offset of the function math channel graph as needed. How close is this to your value from earlier? Set the phase of channel 1 back to zero.
- Measuring Phase: Press the "Measure" button in the top left corner of the oscope. This should bring up the measurement menu. Press the "Time" button and use top knob to select "Phase 1->2 (down)". Press in the top knob to selection this. A green value should appear on the screen and show you the phase between the two channels. Does this agree with what you've found?
- You should note that the phase reading moves around some. That phase measurement is so-so and should really be measured using another device.
- Set the phase for channel 1 to 0 and align the phases of the two channels.
- Signal Sum: Return to the math menu and change the Operate control to "A+B". The purple graph should now show the sum of the two waves.
- Change the frequency of channel 1 to produce a 2Hz beat note in the purple sum signal. How would the signal change if you were look at the difference of these two new waves. Try it.
- Change both channels of the function generator to output 35Hz signals.
- Fourier Transform: Recall that the fourier transform of a time signal gives information about the frequencies that appear in a signal. In the math menu, change the Operate option to "FFT", the Source to CH1, the Display to "Full Screen" and scale to "Vrms". This should display the fourier transform of whatever signal is in channel 1. Note that you can press the CH1 and CH2 buttons twice to turn off the displays for channel 1 and 2 without affecting the math signal.
- FFT Frequency Spacing: With the FFT information at the bottom of the screen, does a peak appear at the frequency you expect? You can use the horizontal scale knob to change the frequency spacing of the fourier transform without affecting the time scaling of the input channels. Change the scale to 5Hz/div to see if the FFT is showing you the correct frequency.
- Horizontal Cursor: There is another way to read values from the display. Press the "Cursor" button so that it lights up. One or two lines should appear on the screen. Use the blue menu buttons to change the Mode to "Manual", the Type to "X", the Source to "FFT" and to highlight only the curl under CurA (i.e. cursor A). Now using the knob at the top of the oscilloscope, move the white line horizontally. You'll note that the box that has appeared on your screen will change values - showing you the frequency at which the cursor is currently set. Overlap cursor A with the peak in your graph. Does it give you correct frequency?
- Hopefully you know that any periodic function of frequency f can be made by summing sine waves with multiples of that frequency with different amplitudes. That is a periodic function, V(t) can be written as
Change the frequency scale to 25Hz/div. Set Channel 1 on the function generator to create a square wave. How does the frequency spectrum on the oscilloscope change? Use cursor 2 to show you the frequency that another other peaks show up at. You may wish to turn the vertical scale knobs to make the spectrum appear bigger and to move the bottom of the spectrum closer to the bottom of the display.- How does the frequency of the 2nd large peak compare to the frequency of the first? Which harmonic of the main frequency is this?
- Do any other large peaks show up? What are their frequencies? What harmonics are those?
- Do you think a square wave contains all harmonics, only even harmonics or only odd harmonics?
- Turn on the channel 1 display and change the time basis to 20ms. Note that this changes the frequency spacing of the FFT greatly. Adjust the frequency basis back to 25Hz/div. You'll also note that the FFT graph looks "smoother". This is because the finest spacing in frequency that the FFT function can display is related to the full-time of the time signal - a shorter time means less fine spacing in frequency.
- Now what harmonics show up in the graph?
- Change the output of channel 1 to a "ramp". What does the channel 1 signal look like - is it a triangle wave or a saw-tooth wave? Which frequency components show in in this waveform?
- Setting Triangle/Saw-tooth Waves On the function generator, when using the ramp waveform, press the blue button under the "Symm" label on the display. Symm sets how symmetric the ramp is. If "Symm" is set to 50%, the function should be a triangle wave - 50% of the "front" half of the signal is the ramp. If "Symm" is 0%, 0% of the "front" half of the signal will be the ramp - that is the ramp will jump from its lowest value to its highest value, then slowly ramp back down to the lowest vale. If Symm is at 100%, the instantaneous jump will occur at the end of the wave. Both the 100% and the 0% Sym settings are saw-tooth waves. These three settings are shown below.
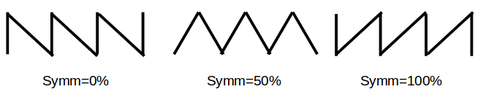 Function Generator Ramp Output (none of which should be confused with the Nine Inch Nails logo)
Function Generator Ramp Output (none of which should be confused with the Nine Inch Nails logo)The Symm method for generating Triangle and Saw-tooth waves is not universal, but is described here in detail to familiarize you with the triangle and saw-tooth waveform.
- Look both the triangle waves and the saw-tooth waves. How do their frequency components, the harmonic content of the wave, compare?
- Vertical Cursor: Press the cursor button and change the "Type" to Y. Now two horizontal lines should appear on the screen. Using the knob at the top of the oscilloscope, you can change the height of each cursor. The values that are listed in the box show you the voltage that the cursor is at.
- Set channel 1 to be a saw-tooth wave (Symm=0% or Symm=100%)
- Use the cursors to read out the heights of the first few harmonics of the saw-tooth wave. (try setting the vertical scale for the FFT plot to 50mVrms/div and the horizontal scale to 25Hz/div).
- How do these heights compare? How do you think the coefficients, , scale as a function of the harmonic, k, for the saw-tooth wave, based on your data?
- Try plotting your data. Measured vs for a bunch of different points and plot it on a computer. Plot the data on a log-log plot and fit a line to this plot. The slope of that line, m, should be how the coefficients scale with k, i.e. .
- Change the waveform in channel 1 to be a triangle wave (Symm=50%). Measure the peak heights for the triangle wave. You may have to change the vertical or horizontal scaling to get better readings of the heights. How do the coefficients scale for the triangle wave?
- Repeat for the sqaure wave.
- Loop up the triangle, square, and sawtooth wave online or in a text book. Did you get the correct forms for the coefficients?
Frequency Sweep
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 35 Hz* | -- |
| Amplitude | 0.5 V | -- |
| Shape | Sine | Off |
| Notes | Will be used in Sweep Mode |
-- |
Connect the output of channel 1 across a resistor and the capacitor in series (so the current would flow through the resistor then through the capacitor). Measure the voltage across the resistor-capacitor pair on channel 1 of the oscilloscope. Measure the voltage across just the capacitor on channel 2 of the oscilloscope. This set up is a frequency filter - it allows some frequencies to pass through the pair while preventing other frequencies, or at least reducing their amplitudes significantly.
- How do the amplitudes of the waves on the oscilloscope compare? Change the frequency of channel 1 by a lot. How does the amplitude change? Do you think high or low frequencies can get through (you should have studied a similar circuit when following the Multimeters module.
- This would be much easier to study if we could look at multiple frequencies in quick succession. So let's do that.
- Frequency Sweep: Press the "Sweep" Button on the function generator (while controlling the output of channel 1). This mode will continually change the output frequency of the generator, allowing us to analyze what happens as the frequency changes.
- Press the button under the "Start" label and set the frequency to 100Hz
- Press the button under the "Stop" label and set the frequency to 300Hz.
- Press the button under the "Time" label and set the time to 1sec.
- The function generator is now set up to constantly (linearly) change the frequency from 100Hz to 300Hz in 1sec. Adjust the horizontal axis on the scope to be 5ms/division. Observe how the waveform changes.
- If you change the direction of the sweep (starting at 300Hz and stopping at 100Hz), how do you think the waveform on the scope will change? Try it.
- Change the scope's trigger to be on channel 2. Adjust the level of the trigger to be around +400mV. Change the sweep's start to 300Hz and end to 65kHz. Yes, that's kilohertz. Adjust the horizontal scale on the function generator to be 100ms/division.
- Trigger Position: Turn the horizontal position knob to move the location of the trigger. Normally, the trigger "starts" at the center of the screen (marked with a pentagon with a "T" in it). Move the trigger to the far left side of the screen. You can now see more of the trace that occurs after the trigger occurs.
- What are you observing on the screen? Does this information tell you if the filter we've built is low-pass or high pass?
- Why do you think you changed the trigger level?
- What do you think would happen if you flip the start and stop points of the sweep? Try it.
- Sweep Scaling: Press the button under the "Linear" label. Press it again until it changes to "Log." This changes the sweep so that it does not change linearly but logarithmically. This is convenient if you'd like to observe how the circuit responds over several orders of magnitude in frequency.
- Change the sweep to go between 10Hz and 80Hz. Change the horizontal axis on the scope to be 50ms.
- Roll Time Basis: Open the horizontal menu on the scope and change the Time Base to Roll. Rather than displaying a full wave form then erasing it to display new data, this mode rolls the data over the screen as it goes. Change between the linear and logarithmic mode for the sweep and see how the form changes as it rolls.
- The roll time basis might be useful for times when you are attempting to minimize/maximize a signal. It will give you a "live" update on what the signal is, while still showing you what the signal was in the recent past.
X-Y Plotting and External Trigger
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 35 Hz | 35 Hz |
| Amplitude | 1.5 V | 1.5 V |
| Shape | Sine | Square |
| Notes | Sync Phases | Used as External Trigger to scope |
Disconnect the two resistors from the function generator. With channel 1, output a sine wave with frequency of 35Hz and amplitude of 1.5V. Connect the output of channel 1 to the diode and one resistor in series. Use the channel 1 of the oscilloscope to measure the voltage across the diode-resistor pair and channel 2 to measure the voltage across just the resistor. These should be set up like the diagram to the right.
Set the frequency and amplitude of channel 2 of the function generator to match that of channel 1. Make channel 2 be a square wave and sync the phases of the two outputs.
- External triggering: Connect the output of channel 2 of the function generator to the External Trigger input of the oscilloscope. In the oscilloscope's trigger menu, set the source to External, Edge triggered, and a down arrow for the direction.
- The external triggering allows you to trigger the scope's data recording without interfering with displaying two different voltage signals. This is useful, for example, when measuring the voltage across a resistor and a capacitor in an RC circuit as there will be a phase different between the voltages.
- The edge triggering is best for square pulses as it just relies on the signal going from high-to-low (or low-to-high). Using the slope setting for square waves cause issues as the slope when a square wave changes is infinite. For non-square waves, this will behave identically to the slope triggering, but not vice-versa.
- Set the vertical scale of both oscilloscope channels to 500mV and the horizontal scale to 5ms. How do the two graphs of the voltage out of the function generator (channel 1) and the voltage dropped across the resistor compare (channel 2) compare?
- Change the vertical offset of channel 2 on the oscilloscope to force the graphs to overlap as much as you can. What must be true about the voltage across the diode so that current flows through it? About what voltage is needed?
- Cursors: Track Mode: Open the cursor menu and set the mode to "Track". When using this mode, the cursor(s) will follow the voltage in a channel and show you time and voltage information at the same time.
- Set the "Cursor A" control to CH2 and move the cursor to the "corner" where the voltage turns on or off. You can eye-ball it, or move watch the "A->Y" chart value goes above 0V.
- Set the "Cursor B" control to CH1 and move this cursor so that the "|ΔX|" value in the chart is 0s. Here, the time-separation between the two cursors is zero.
- What is the voltage read at cursor B (the "B-> Y" value in the chart)? This is the minimum voltage needed for current to flow through the resistor.
- X-Y Time Basis: Press the "Menu" button in the middle of the horizontal control column. Use the menu buttons to change the "Time Base" from Y-T to X-Y. This shows the voltage in channel 1 plotted along the x-axis and the voltage in channel 2 plotted along the y-axis.
- You'll note that the cursor menu changes from track mode - while using the X-Y time basis, you cannot use track mode.
- Adjusting Horizontal Axis in X-Y Basis: Using the horizontal adjustment knobs does not change the horizontal axis in the X-Y basis. To do this, press the channel 1 button to open the channel 1 adjustment menu. Use the vertical adjustment knobs to change the scale/center of the voltage for channel 1 - and hence the horizontal axis in the X-Y basis.
- Adjusting Vertical Axis in X-Y Basis: Open the channel 2 adjustment menu. Use the vertical adjustment knobs to change the scale/center of the voltage for channel 2 - and hence the vertical axis in the X-Y basis.
- Adjust the axes so as much of the graph shows up on the oscilloscope.
- Sampling in the X-Y basis: The graph for the X-Y mode will probably be "moving around". This is due to a mismatch between the oscillation frequency and the sampling rate of the oscilloscope. You can use the horizontal scale knob to adjust the sampling rate until you can see the entire range of the data you are plotting.
- Use vertical cursors find the input voltage (channel 1 voltage) that causes current to start to flow through the diode and to the resistor. Estimate the voltage at which the out voltage follows ohm's law through the resistor. This is the "forward" voltage for the diode. Does your measured value agree with the value from the [diode's data sheet].
Noise and Averaging
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 35 Hz | 35 Hz* |
| Amplitude | 0.5 V | 0.5 V |
| Shape | Sine | Noise* |
| Notes | -- | -- |
Build the following circuit: Connect the positive (red) outputs of both channels to one end of different resistors (resistors 1 and 2). The other end of each resistor should be connected to one end of a third resistor (one end of all three resistors should touch). Connect the black outputs of both channels to free end of the third resistor (resistor 3). This circuit is shown to the right, along with a simplified "standard" circuit drawing.
This is a (crude) voltage summer: the voltages from the two output channels will add together in the third resistor. This is not a very good voltage summer, as the output voltage in the third resistor isn't just the sum, but sum of the two voltages each scaled by some factor (related to the resistances). There are much better ways to sum voltages, but this will work fine for our purposes.
Connect the input of channel 1 of the oscilloscope to the voltage across resistor 1 and the input of channel 2 of the oscilloscope to the voltage across resistor 3. Set the scope to trigger on channel 1 and set the horizontal scale so that a few wave forms show on the display. Adjust the vertical scales of each channel as you feel appropriate.
- Have both channels output sine waves and align the phases of the function generator output.
- How does the signal in channel 2 (the sum(ish) of the two signals) compare when you adjust the phase of channel 2?
- Noise Generation: Select channel 2 control on the function generator and press the "Noise" button. This will generate a random noise-y signal output. Note which wave properties you can change while in noise mode.
- Observe the voltage across resistor 2 on channel 2 oscilloscope, see how noisy it is?
- Return the output of channel 2 to measure the voltage across resistor 3.
- Adjust the amplitude of the noise signal and note how the summed signal changes on the oscilloscope. Return the amplitude to 0.5V.
- Averaging Signals: Press the "Acquire" button on the oscilloscope. Change the "Acquisition" item in the menu to "Average".
- This setting displays the average of the previous N scope traces (N is set in the "Averages" menu item that appears). Each time you change any setting on the scope, the average must be recalculated.
- Adjust the number of averages and observe how the signal changes. Set the number of averages to 4.
- Change the amplitude of the sine wave of channel 1 to 1.0V. Note how long it takes for the signal to "adjust" on the oscilloscope. Repeat this with the number of averages set to 32. How does the time for the signal to "adjust" compare to setting the averages to 4?
- Return the acquisition mode to normal.
- Try changing the amplitude of the noise signal in channel 1. What happens to the summed (and averaged) signal. Why do you think this would happen?
- Display the fourier transform of channel 2 on the oscilloscope. Adjust the amplitudes of both channels of the function generator and observe changes in the 35Hz peak. Repeat this after turning on signal averaging.
Oscilloscope Time Properties
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 50 Hz* | 50 Hz |
| Amplitude | 0.5 V | 0.5 V |
| Shape | Sine | Sine |
| Notes | -- | -- |
Construction 2 copies of circuit 1, one for each output of the function generator. Use scope channel 1 to read the voltage output from channel 1 of the oscilloscope. Use scope channel 2 to read the voltage output from channel 2 of the oscilloscope.
- Oscilloscope Sample Rate: Open the horizontal menu on the oscilloscope. Change the horizontal scale to 10ms. Note that as you change the time, the "Sa Rate" menu item changes. This tells you the sample rate of the oscilloscope - how many voltages it saves every second. Note that as you go to shorter times, the scope must record MORE samples do account for the fine time resolution you are asking it to display.
- Set the time scaling to 10ms.
- On a piece of paper, draw five complete sine waves.
- Let's say that this wave is recorded by the oscilloscope at a rate equal to its frequency - that is for every each complete wave, the oscilloscope records ONE data point. On your wave, put an x at each recorded data point - make sure these data points are equally spaced horizontally.
- Draw a curve connecting these data points - this is the plot that the oscilloscope would show you.
- How similar is this plot to the actual wave you drew?
- Repeat the steps using a sampling rate that is a half and twice the frequency of your drawn wave (1 data point recorded for every 2 complete waves and 2 data points recorded for every complete wave).
- What can you conclude about the above? How should the sample rate of your oscilloscope compare to the frequency of your signal such that you get a reliable trace on the scope?
- What you've drawn and discovered is called aliasing, no let's observe it with the scope.
- With 10ms scaling, what is the sample rate of your scope? Make sure the scope is triggered on channel 2 and change the frequency of channel 1 to the match the sample rate. Does the scope display a similar graph to what you've drawn?
- Set the frequency to twice your sample rate (so that the sample rate is half the frequency). What does the graph look like? Does this agree with what you drew?
- Set the frequency to half your sample rate (so the sample rate is twice the frequency). What does the graph look like? Does this agree with what you drew? (The frequency should be really large, so that many, many completed waves should appear on the screen - they should all merge together and just look like a thick band).
- Why do the graphs on the oscilloscope change, rather than just stay stationary?
Termination
| Channel 1 | Channel 2 | |
|---|---|---|
| Frequency | 20 Hz | -- |
| Amplitude | 0.5 V | -- |
| Shape | Sine | OFF |
| Notes | -- | -- |
Build the circuit to the right - a voltage divider. The input voltage (from the function generator) is split between the two resistors (relative to their resistances). When the resistors are the same resistance, the voltage dropped across each resistor is half the input resistance. More specifically, the resistance across the 2nd resistor is
- Test the above equation by comparing the input voltage (, voltage across both resistors) and the voltage across the 2nd resistor. Use horizontal cursors to check the voltages on each channel.
- Measurement Menu: Press the "Measure" button on the screen. This menu gives a large variety of voltage and time measurement options for a channel. It will display the measured results at the bottom of the screen.
- Set the source to Channel 1.
- Press the voltage button and navigate the menu to select "Vamp". To move the cursor, use the selection knob and you can select an option either by pressing the knob in or by pressing the button next to Voltage again. A measurement value should appear on the bottom of the screen and will tell you the amplitude of the measured signal (in this case the amplitude is defined to be the peak-to-peak voltage of the sine wave).
- Change the source to channel 2 and display the peak-to-peak voltage for channel 2.
- How do these amplitudes compare? Do they agree with the equation above, assuming the resistances of the resistors are (almost) equal.
- The "clear" button will remove the measurements from the screen, although you should keep the measurement values on the screen for now.
- Terminator: Add a voltage terminator between the BNC-to-banana-plug adapter and the input of channel 2 of the oscilloscope. Set the termination resistance to 50ohms.
- What happens to the amplitude to the voltage in channel 1? If the measured amplitude changes to a series of asterisks you'll have to change the vertical scale for channel 1 in order to measure the amplitude.
- Change the termination resistance. How does the measured voltage change? Does the measured voltage get closer to what you expect (from the equation above) when the terminator's resistance gets larger or smaller?
- The oscilloscope has an input resistance, that is there is a resistor connecting the positive and negative inputs of each channel of the oscilloscope. What is that resistance (it can be read from the front of the oscilloscope)? With your answer from the previous question, does this lead you to trust the voltage readings of the oscilloscope without a terminator?
- The termination resistance (or the input resistance of the oscilloscope) and the 2nd resistor in the voltage divider are acting in parallel, such that the termination resistance is acting as a load on the voltage divider - that is some extra electrical component that the voltage divider is supplying voltage for. The effective resistance of the two resistors in parallel is .
- For a very small termination resistance (), how does the effective resistance, compare to the two resistances, and ? How would affect the voltage across resistor 2 above?
- If the termination resistance is much larger than the resistance of resistor 2 (), how does the effective resistance, compare to the two resistances, and ? How would affect the voltage across resistor 2 above?
- For using the oscilloscope to measure voltages in a circuit, do you think having a larger or smaller termination voltage would be preferred? Why?
- To look at the effects of the terminator more carefully, let's remove the voltage divider entirely: connect the output of channel 1 of the function generator to the terminator and then directly to the oscilloscope.
- The function generator output also has a resistance between the positive and negative outputs of each channel. What is this resistance (it is on the front of the function generator)?
- Set the resistance of the terminator to match the resistance of the function generator. How does the amplitude of the wave measured on the oscilloscope compare to the amplitude that you have set on the function generator?
- The matched resistances (output of function generator and input of oscilloscope) are acting as a voltage divider. According to the equation above, are you measuring what you expect with the oscilloscope?
- Matching the resistances is called impedance matching (recall that impedance is sort of a generalized resistance for resistors, capacitors, and inductors). Impedance matching is important for carefully measuring signals - especially those that are oscillating.
- Similar to when light enters a medium with a different index of refraction, when electric waves in a wire reaches an object with a different impedance the wave can partially reflect backwards down the wire.
- If an electrical signal is traveling between two objects with different impedances, the signal can repeatedly reflect from each object, seriously impacting the signal seen by each object.
- Impedance matching avoids this problem, but as a result, divides the measured voltage in half. For this reason, terminators are often labeled with having "3dB attenuation" as halving a signal is a 3 decibel decrease (review wikipedia's article on decibels).
- For example, individual photons can be measured by many devices, including an Avalanche Photo-Diode (APD). These will convert a photon it sees into a very short (nanosecond long) electric pulse. Counting these pulses with a device that is not properly impedance matched to the APD can result in photon counts that are too high - a portion of the electron pulse is reflected back to the APD, then back towards the counting device and counted a 2nd time. This can repeat a number of times, giving photon counts that are much higher than are actually being detected.
- Often, oscilloscopes have settings that can change the input impedance of the oscilloscope (note that the oscilloscope you are using does not). This allows you to easily set up the scope for making appropriate measurements.
Exporting Data
With the function generator, sine wave with an amplitude of 0.8V and frequency 715 Hz. Use the measure menu to display the RMS voltage of the signal from the function generator. Record a single trace of this wave on the oscilloscope, showing at least 12 complete waves.
- Exporting Data Insert a USB storage device into the USB slot on the front of the oscilloscope.
- Press the Storage button and change the storage menu item to CSV.
- Set the Data Depth to Displayed.
- Press the blue menu button next to "External". This will open a menu that should show you to file system of the USB drive. Use the menu buttons to change to whatever location on the drive you would like and then press the Save button. You can name the file whatever you'd like.
- Press the back button (arrow at the bottom of the menu) until you return to the storage menu's top level. Change the data depth to Maximum and save the data again (as a different file name than before, of course).
- After the file is done saving, you can remove the USB device.
- Plug the USB device into a computer. Open the two CSV files with a text document reader (not a spreadsheet program). How is the data saved? Is the data saved as tab- or comma-deliminated (tabs or commas separate columns).
- Open the files in a spreadsheet program (LibreOffice Calc is available on the computers in the advanced projects lab). When the program asks about importing data, make sure that the correct delimination is selected.
- Plot the two sets of data as X-Y scatter plots. What is the difference between the "Displayed" (first file saved) and the "Maximum" data depth options?
- Calculate the RMS voltage of the data.
- In LibreOffice Calc, you can use the functions sumsq(), sqrt(), and count() to calculate the RMS voltage. sumsq() calculates the sum of the squares of the data points given, count() gives the number of non-empty cells in the defined region, and sqrt() calculates the square root of its input.
- Does this agree with the RMS voltage given by the oscilloscope?
- How does it compare to the amplitude of the sine wave? Try dividing by the value you set the amplitude to.