Difference between revisions of "Permittivity and Permeability of Materials Obstacle Course"
(→* Permittivity of a Lossy Material From a Capacitance Measurement) |
(→Activities) |
||
| Line 37: | Line 37: | ||
=== * A Better Permittivity-Capacitance Measurement of a ''Lossless'' Material === | === * A Better Permittivity-Capacitance Measurement of a ''Lossless'' Material === | ||
| + | |||
| + | coming soon... | ||
[[File:Epsiloncap2.png |right |350px]] | [[File:Epsiloncap2.png |right |350px]] | ||
| Line 59: | Line 61: | ||
## Do the above procedure for at least three frequencies between 10 MHz and 50 MHz. | ## Do the above procedure for at least three frequencies between 10 MHz and 50 MHz. | ||
## Plot <math>\epsilon'_r</math> and <math>\epsilon''_r</math> as a function of frequency. | ## Plot <math>\epsilon'_r</math> and <math>\epsilon''_r</math> as a function of frequency. | ||
| + | |||
| + | === Waveguide Techniques(above 50MHz) === | ||
| + | coming soon... | ||
Revision as of 10:57, 21 May 2018
PAGE UNDER CONSTRUCTION
Contents
- 1 Permanent Materials
- 2 Materials to Borrow When Necessary
- 3 Activities
- 3.1 Reading
- 3.2 Capacitance Techniques (Below 10MHz)
- 3.3 * Permittivity of a Lossless Material From a Capacitance Measurement
- 3.4 * A Better Permittivity-Capacitance Measurement of a Lossless Material
- 3.5 * Permittivity of a Lossy Material From a Capacitance Measurement (up to 50 MHz)
- 3.6 Waveguide Techniques(above 50MHz)
Permanent Materials
- 6061 3/8" Al rod stock
- Teflon
- Glass microscope slide
- HP Signal Generator (DC-1 GHz)
- Oscilloscope (at least 1GHz bandwidth)
- Miscellaneous electrical components
Materials to Borrow When Necessary
- Milling machine
- Lathe
Activities
Reading
- Read the Wikipedia articles on permittivity and permeability. With the help of the instructor or TA try to achieve a physical understanding of just what the permittivity and permeability mean in a bulk material.
- Read the first three sections of this paper (pages 1-27). Pay particular attention to the permittivity (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} ) / capacitance and permeability () / inductance associations.
Capacitance Techniques (Below 10MHz)
* Permittivity of a Lossless Material From a Capacitance Measurement
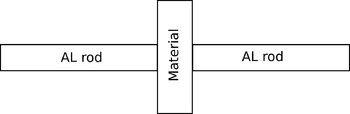
- Place three samples (air, Teflon, glass) between the aligned and polished ends of two 3/8" diameter, 1/2" lengths of 6061 Al rods (as shown at right). should be on the order of 1 mm. Measure the capacitances and, from the known surface area and spacing , determine the material's relative permittivity. (for a capacitor with no fringing fields).
- How do your measured permittivity values compare to standard reference values?
- Use this web applet to build a capacitor and observe the field lines . Are there fringing fields?
(air): 1.000536
(Teflon): 2.1
(glass): 3.7-10
* A Better Permittivity-Capacitance Measurement of a Lossless Material
coming soon...
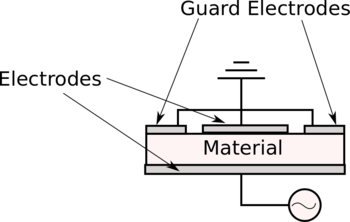
- Use this web applet to build a guarded-electrode capacitor (as shown at the right) and observe the field lines . Are there fringing fields?
- Measure the three permittivities (air, Teflon, glass) again using this guarded-electrode setup.
- How do these results compare to your first (unguarded) measurements?
- How do these results compare to the standard values?
The measurements above for a lossless material amount to requiring the permittivity to be real (as opposed to complex). However, for a lossy material, the permittivity is complex and we need an additional characteristic (beyond simply the capacitance) to characterize the material. This additional characteristic is the conductance . The measurement below will include the conductance of the material.
* Permittivity of a Lossy Material From a Capacitance Measurement (up to 50 MHz)
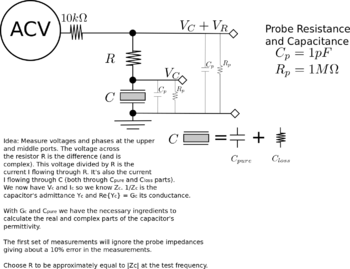
- Employ the guarded-electrode setup above and measure the lossy material's capacitance and conductance. and , where are, respectively, the real and imaginary parts of the complex permittivity.
- Simultaneously measure the voltage across the resistor and Lock-in voltage at . Employ a lock-in time constant that is much longer than the period of the AC driving voltage. The lock-in voltage is given by , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{out}} is the voltage across the capacitor and is the phase difference between the AC driving voltage and
- The current through the capacitor is given by . The voltage across the capacitor is given by , where is the capacitor's impedance. Solve for the impedance .
- The capacitor's admittance is given by , where the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Re(Y_C)=G} (the conductance) and the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Im(Y_C)=B} (the susceptance). Calculate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} .
- Read section 13.1 (pages 106-107) in this [paper].
- Calculate the relative permittivity Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_r} as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon'_r=\frac{C}{C_{air}}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon''_r=\frac{G}{\omega C_{air}}} .
- Do the above procedure for at least three frequencies between 10 MHz and 50 MHz.
- Plot Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon'_r} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon''_r} as a function of frequency.
Waveguide Techniques(above 50MHz)
coming soon...